در مبحث قبلی، در مورد چگونگی کاهش ابعاد ماتریس ویژگی مسئله با ساختن ویژگی های جدید با همان توانایی مشابه ویژگی های قبلی اما با ابعاد کمتر به منظور آموزش با کیفیت مدل یادگیری ماشین، بحث کردیم. به این عمل استخراج ویژگی گفته می شود. در این مبحث یک رویکرد دیگر را پوشش خواهیم داد: انتخاب ویژگی های آموزنده با کیفیت بالا و حذف ویژگی های کم کاربرد. به این روش انتخاب ویژگی می گویند. انتخاب ویژگی ها و کاهش ابعاد به ما این امکان را می دهد تعداد ویژگی های یک مجموعه داده را فقط با حفظ ویژگی های مهم به حداقل برسانیم. به عبارت دیگر، ما می خواهیم ویژگی هایی را که حاوی مفید ترین اطلاعاتی است که مدل ما برای پیش بینی دقیق نیاز دارد را حفظ کنیم، در حالی که ویژگی های زائد را که حاوی اطلاعات اندکی هستند و یا هیچ اطلاعاتی ندارند را حذف کنیم، پیش بینی دقیق می کنیم.
سه نوع روش انتخاب ویژگی وجود دارد: filter، wrapper و embedded. روشهای filter با بررسی خصوصیات آماری ویژگی ها بهترین آن ها را انتخاب می کنند. روش های wrapper با استفاده از آزمون و خطا زیر مجموعه ویژگی هایی را تولید می کنند که مدل هایی با بالاترین پیش بینی ها را تولید می کنند و روش های embedded بهترین زیر مجموعه ویژگی را به عنوان توسعه فرایند آموزش الگوریتم یادگیری انتخاب می کنند.
ما هر سه روش را در این بخش توضیح می دهیم. اما به دلیل این که روش های embedded با الگوریتم های یادگیری ماشین کاملاً هم پوشانی دارند، توضیح آنها قبل از وارد شدن عمیق تر به مبحث الگوریتم ها دشوار است. بنابراین، در این بخش فقط روش های انتخاب ویژگی filter و wrapper را پوشش می دهیم و روش های embedded خاص را جلوتر که الگوریتم های یادگیری ماشین به طور مفصل بحث می شوند، توضیح می دهیم.
واریانس ویژگی عددی با استفاده آستانه گذاری (Thresholing)
چگونگی حذف ویژگی های کم واریانس (ویژگی هایی با اطلاعات کم) وقتی مجموعه ای از ویژگی های عددی داریم:
یک Threshold برای واریانس در نظر می گیریم و ویژگی هایی را که واریانس آن ها بالاتر از Threshold است را انتخاب می کنیم.
# Load libraries from sklearn import datasets from sklearn.feature_selection import VarianceThreshold # import some data to play with iris = datasets.load_iris() # Create features and target features = iris.data target = iris.target # Create thresholder thresholder = VarianceThreshold(threshold=.5) # Create high variance feature matrix features_high_variance = thresholder.fit_transform(features) # View high variance feature matrix features_high_variance[0:3] array([[ 5.1, 1.4, 0.2], [ 4.9, 1.4, 0.2], [ 4.7, 1.3, 0.2]])
آستانه واریانس یا Variance thresholding (VT) یکی از بارزترین روش ها برای انتخاب ویژگی است. در واقع این روش میگوید ویژگی ها با واریانس کم نسبت به ویژگی ها با واریانس زیاد دارای اطلاعات کمتر و مفید تری هستند. VT ابتدا واریانس هر ویژگی را محاسبه می کند:
operatornameVar(x) =
x بردار ویژگی، xi یک مقدار ویژگی منحصر به فرد و μ مقدار میانگین آن ویژگی است. سپس، ویژگی هایی که واریانس آن ها ازمقدار آستانه کمتراست را حذف می کند.
هنگام استفاده از VT باید به دو نکته دقت کرد: اول، واریانس مرکز نیست، یعنی در واحد مربع خود ویژگی است. بنابراین، وقتی مجموعه ویژگی ها دارای واحدهای مختلف باشند (مثلا، یک ویژگی اعداد سال است در حالی که ویژگی دیگرقیمت دلار است) VT کار نخواهد کرد. دوم، آستانه واریانس به صورت دستی انتخاب می شود، بنابراین برای انتخاب مقدار خوب باید از اطلاعات خود استفاده کنیم. با استفاده از variances_ می توان واریانس هر ویژگی را مشاهده کرد:
# View variances thresholder.fit(features).variances_ array([ 0.68112222, 0.18675067, 3.09242489, 0.57853156])
در آخر، اگر ویژگی ها استاندارد شده باشند (به معنی واریانس واحد و صفر)، واضح است که آستانه درست کار نخواهد کرد:
# Load library from sklearn.preprocessing import StandardScaler # Standardize feature matrix scaler = StandardScaler() features_std = scaler.fit_transform(features) # Caculate variance of each feature selector = VarianceThreshold() selector.fit(features_std).variances_ array([ 1., 1., 1., 1.])
واریانس ویژگی باینری با استفاده از آستانه گذاری (Thresholding)
چگونگی حذف ویژگی های دارای واریانس کم (حای اطلاعات کم) وقتی مجموعه ی ویژگی های باینری داریم:
یکThreshold برای واریانس در نظر می گیریم با استفاده از متغیر تصادفی برنولی ویژگی هایی که واریانس آنها بالاتر آستانه هستند را انتخاب می کنیم.
# Load library from sklearn.feature_selection import VarianceThreshold # Create feature matrix with: # Feature 0: 80% class 0 # Feature 1: 80% class 1 # Feature 2: 60% class 0, 40% class 1 features = [[0, 1, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1], [1, 0, 0]] # Run threshold by variance thresholder = VarianceThreshold(threshold=(.75 * (1 - .75))) thresholder.fit_transform(features) array([[0], [1], [0], [1], [0]])
همانند ویژگی های عددی، یک استراتژی برای انتخاب ویژگی های بهتر و با کیفیت، بررسی واریانس آنها است. در ویژگی های باینری (متغیرهای تصادفی برنولی)، واریانس به صورت زیر محاسبه می شود:
Var(x) = p(1-p)
p نسبت مشاهدات کلاس 1 است. با تنظیم p، می توانیم ویژگی هایی را که اکثرا مشاهدات یک کلاس هستند را حذف کنیم.
مدیریت ویژگی های بسیار مرتبط باهم
چگونگی انتخاب ویژگی وقتی یک ماتریس ویژگی دارید و گمان می کنید برخی از ویژگی ها بسیار با هم مرتبط هستند:
برای بررسی ویژگی های بسیار مرتبط با هم از ماتریس همبستگی استفاده می کنیم. اگر ویژگی های بسیار مرتبط با هم وجود داشته باشد، در نظر گرفتن یکی ازاون ویژگی ها کافی است.
# Load libraries import pandas as pd import numpy as np # Create feature matrix with two highly correlated features features = np.array([[1, 1, 1], [2, 2, 0], [3, 3, 1], [4, 4, 0], [5, 5, 1], [6, 6, 0], [7, 7, 1], [8, 7, 0], [9, 7, 1]]) # Convert feature matrix into DataFrame dataframe = pd.DataFrame(features) # Create correlation matrix corr_matrix = dataframe.corr().abs() # Select upper triangle of correlation matrix upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(np.bool)) # Find index of feature columns with correlation greater than 0.95 to_drop = [column for column in upper.columns if any(upper[column] > 0.95)] # Drop features dataframe.drop(dataframe.columns[to_drop], axis=1).head(3)
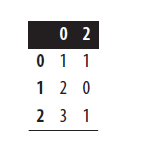
یک مشکل که ما اغلب در یادگیری ماشین با آن روبرو می شویم ویژگی های بسیار همبسته یا مرتبط با هم هستند. اگر دو ویژگی بسیار با هم ارتباط داشته باشند، اطلاعات موجود در آنها بسیار شبیه به هم است و احتمالاً یکی از آن ها زائد است. که ساده ترین راه این است که یکی از آنها را از مجموعه ویژگی ها حذف کنید.
ابتدا یک ماتریس همبستگی از همه ویژگی ها ایجاد می کنیم:
# Correlation matrix dataframe.corr()
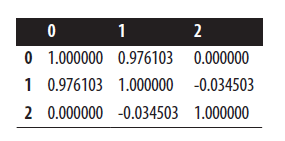
سپس به مثلث بالایی ماتریس همبستگی نگاه می کنیم تا جفت ویژگی های بسیار همبسته را شناسایی کنیم:
# Upper triangle of correlation matrix upper
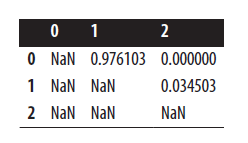
در آخر، یکی از این جفت ویژگی ها را از مجموعه ی ویژگی ها حذف می کنیم.
حذف ویژگی های نامربوط برای طبقه بندی
چگونگی حذف ویژگی هایی که اطلاعات کافی و مرتبط ندارند وقتی یک بردار هدف طبقه بندی شده دارید:
اگر ویژگی ها طبقه بندی شده باشند، یک chi-square (χ2) بین هر ویژگی و بردار هدف را محاسبه کنید:
# Load libraries
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2, f_classif
# Load data
iris = load_iris()
features = iris.data
target = iris.target
# Convert to categorical data by converting data to integers
features = features.astype(int)
# Select two features with highest chi-squared statistics
chi2_selector = SelectKBest(chi2, k=2)
features_kbest = chi2_selector.fit_transform(features, target)
# Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kbest.shape[1])
Original number of features: 4
Reduced number of features: 2
اگر ویژگی ها کمی بودند، مقدار ANOVA F-value را بین هر ویژگی و بردار هدف محاسبه کنید:
# Select two features with highest F-values
fvalue_selector = SelectKBest(f_classif, k=2)
features_kbest = fvalue_selector.fit_transform(features, target)
# Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kbest.shape[1])
Original number of features: 4
Reduced number of features: 2
به جای انتخاب کردن تعدادی ویژگی خاص، می توانیم از SelectPercentile برای انتخاب n درصد از بهترین ویژگی ها استفاده کنیم:
# Load library
from sklearn.feature_selection import SelectPercentile
# Select top 75% of features with highest F-values
fvalue_selector = SelectPercentile(f_classif, percentile=75)
features_kbest = fvalue_selector.fit_transform(features, target)
# Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kbest.shape[1])
Original number of features: 4
Reduced number of features: 3
Chi-square استقلال دو بردار طبقه بندی را بررسی می کند. یعنی، تفاوت بین تعداد داده های مشاهده شده در هر کلاس از ویژگی طبقه بندی شده و این که آن ویژگی مستقل باشد یعنی هیچ ارتباطی با بردار هدف نداشته باشد.
فرمول
Oi تعداد داده ها در کلاس i است و Ei تعداد داده ها در کلاس i است که اگر رابطه ای بین ویژگی و بردار هدف وجود نداشته باشد، نشان می دهد.
Chi-square یک عدد واحد است که به شما می گوید چه مقدار تفاوت بین تعداد مشاهده شما و تعدادی که شما در صورت عدم وجود هیچ رابطه ای در جمعیت انتظار دارید. با محاسبه Chi-square بین یک ویژگی و بردار هدف، میتوانیم استقلال بین این دو را اندازه گیری کنیم. اگر هدف از متغیر ویژگی مستقل باشد، برای اهداف ما بی ربط است زیرا حاوی هیچ اطلاعاتی نیست که بتوانیم از آن برای طبقه بندی استفاده کنیم. از طرف دیگر، اگر این دو ویژگی به شدت وابسته باشند، برای آموزش مدل ما بسیار مهم هستند.
به منظوراستفاده از Chi-square برای انتخاب ویژگی، Chi-square را بین هر ویژگی و بردار هدف به دست می آوریم سپس ویژگی ها را با بهترین Chi-square انتخاب می کنیم. در کتابخانه scikit-learn، می توانیم از SelectKBest برای انتخاب ویژگی با بهترین Chi-square استفاده کنیم. پارامتر k تعداد ویژگی هایی را که می خواهیم نگه داریم را تعیین می کند.
یک نکته مهم این است که Chi-square تنها بین دو بردار دسته بندی قابل محاسبه است. به همین دلیل، Chi-square برای انتخاب ویژگی ها هم به بردار هدف و هم به ویژگی های طبقه بندی شده نیاز دارد. با این حال، اگر یک ویژگی عددی داشته باشیم، می توانیم ابتدا با تبدیل ویژگی کمی به یک ویژگی طبقه بندی، از روش Chi-square استفاده کنیم. سپس برای استفاده از روش Chi-square ، همه مقادیر باید غیرمنفی باشند.
اگر یک ویژگی عددی داشته باشیم می توانیم از f_classif برای محاسبه ANOVA F-value برای هر ویژگی و بردار هدف استفاده کنیم. مقدار F-value نشان می دهد وقتی ویژگی عددی که بر اساس بردار هدف گروه بندی می کنیم، میانگین هر گروه خیلی تفاوت دارد یا خیر. به عنوان مثال، اگر یک بردار هدف باینری مثل جنسیت و یک ویژگی کمی مانند نمرات آزمون داشته باشیم، مقدار F-value به ما می گوید که آیا میانگین نمره آزمون برای مردان با میانگین نمره آزمون برای زنان متفاوت است یا خیر، اگر متفاوت نباشد، نمره آزمون به ما کمک نمی کند جنسیت را پیش بینی کنیم، بنابراین ویژگی بی ربطی است.
حذف ویژگی ها به صورت بازگشتی
چگونگی نگه داشتن بهترین ویژگی ها به صورت خودکار:
در کتابخانه scikit-learn از متد RFECV برای حذف ویژگی به روش بازگشتی یا recursive feature elimination (RFE) به وسیله اعتبار سنجی متقابل یا cross-validation (CV) استفاده کنید. یعنی مرتباً یک مدل را train کنید، هر بار یک ویژگی را حذف کنید تا عملکرد مدل (مثلاً دقت) بدتر شود اینطوری سایر ویژگی ها بهترین هستند:
# Load libraries import warnings from sklearn.datasets import make_regression from sklearn.feature_selection import RFECV from sklearn import datasets, linear_model # Suppress an annoying but harmless warning warnings.filterwarnings(action="ignore", module="scipy", message="^internal gelsd") # Generate features matrix, target vector, and the true coefficients features, target = make_regression(n_samples = 10000, n_features = 100, n_informative = 2, random_state = 1) # Create a linear regression ols = linear_model.LinearRegression() # Recursively eliminate features rfecv = RFECV(estimator=ols, step=1, scoring="neg_mean_squared_error") rfecv.fit(features, target) rfecv.transform(features) array([[ 0.00850799, 0.7031277 , -1.2416911 , -0.25651883, -0.10738769], [-1.07500204, 2.56148527, 0.5540926 , -0.72602474, -0.91773159], [ 1.37940721, -1.77039484, -0.59609275, 0.51485979, -1.17442094], ..., [-0.80331656, -1.60648007, 0.37195763, 0.78006511, -0.20756972], [ 0.39508844, -1.34564911, -0.9639982 , 1.7983361 , -0.61308782], [-0.55383035, 0.82880112, 0.24597833, -1.71411248, 0.3816852 ]])
هنگامی که RFE را انجام دادیم، می توانیم تعداد ویژگی هایی که باید حفظ کنیم را مشاهده کنیم:
# Number of best features rfecv.n_features_ 5
همچنین می توانیم ببینیم که کدام یک از این ویژگی ها را باید حفظ کنیم:
# Which categories are best rfecv.support_ array([False, False, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, False, False, False, False, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False], dtype=bool)
حتی می توانیم رتبه بندی ویژگی ها را مشاهده کنیم:
# Rank features best (1) to worst rfecv.ranking_ array([11, 92, 96, 87, 46, 1, 48, 23, 16, 2, 66, 83, 33, 27, 70, 75, 29, 84, 54, 88, 37, 42, 85, 62, 74, 50, 80, 10, 38, 59, 79, 57, 44, 8, 82, 45, 89, 69, 94, 1, 35, 47, 39, 1, 34, 72, 19, 4, 17, 91, 90, 24, 32, 13, 49, 26, 12, 71, 68, 40, 1, 43, 63, 28, 73, 58, 21, 67, 1, 95, 77, 93, 22, 52, 30, 60, 81, 14, 86, 18, 15, 41, 7, 53, 65, 51, 64, 6, 9, 20, 5, 55, 56, 25, 36, 61, 78, 31, 3, 76])
این روش تا اینجا پیشرفته ترین دستورالعمل موجود در این بخش است، که ترکیبی از موضوعاتی است که هنوز به تفصیل به آنها نپرداخته ایم، ولی به اندازه کافی ساده است که دراین قسمت آورده ایم. ایده RFE این است که مدلی را آموزش دهیم که شامل برخی پارامترها (وزن یا ضرایب نامیده می شود) مانند رگرسیون خطی یا ماشین های بردار پشتیبان (SVM) باشد. دفعه اولی که مدل را آموزش می دهیم، همه ویژگی ها را در بر می گیریم سپس، ویژگی را با کوچکترین پارامتر پیدا می کنیم (این ویژگی ها مقیاس بندی شده یا استاندارد هستند)، به این معنی که از اهمیت کمتری برخوردار است و ویژگی را از مجموعه ویژگی ها حذف می کنیم.
سوالی که اینجا پیش می آید این است: چند ویژگی را باید حفظ کنیم؟ می توانیم به صورت فرضی این حلقه را تکرار کنیم تا زمانی که فقط یک ویژگی برای ما باقی بماند. یک رویکرد بهتر این است که ما مفهوم جدیدی به نام اعتبارسنجی متقابل cross-validation (CV) را در نظر بگیریم. در این مورد در بخش های جلو مفصل توضیح خواهیم داد.
با توجه به داده هامون یعنی 1- هدفی که می خواهیم پیش بینی کنیم و 2- ماتریس ویژگی، ابتدا داده ها را به دو گروه تقسیم می کنیم: یک مجموعه آموزش و یک مجموعه تست. دوم، مدل خود را با استفاده از مجموعه آموزش train می کنیم. سوم، فرض می کنیم که هدف یا کلاس مجموعه تست را نمی دانیم و برای پیش بینی مقادیر مجموعه تست، مدل خود را بر روی ویژگی های مجموعه تست اعمال می کنیم. در آخر، مقادیر هدف پیش بینی شده خود را با مقادیر هدف واقعی مقایسه می کنیم تا مدل خود را ارزیابی کنیم.
می توانیم از CV استفاده کنیم تا تعداد بهینه ویژگی هایی که می توان در هنگام RFE نگه داشت را پیدا کنیم. در کل، در RFE با CV پس از هر بار تکرار، برای ارزیابی مدل خود از cross-validation (CV) استفاده می کنیم. اگر CV نشان دهد که پس از حذف ویژگی، مدل بهتر کار می کند، به حلقه بعدی ادامه می دهیم. ولی، اگر CV نشان دهد که مدل ما بعد از حذف ویژگی بدتر شده است، آن ویژگی را دوباره در مجموعه ویژگی ها قرار می دهیم و آن ویژگی ها را به عنوان بهترین انتخاب می کنیم.
برای پیاده سازی RFE با CV در کتابخانه scikit-learn ، با نام RFECV می باشد و شامل تعدادی پارامتر مهم است. پارامتر estimator نوع مدلی که می خواهیم آموزش بدهیم مشخص می کند (به عنوان مثال ، رگرسیون خطی). step regression تعداد یا نسبت ویژگی هایی را که طی هر حلقه کاهش می یابد را تنظیم می کند. پارامتر scoring معیار کیفیتی است که برای ارزیابی مدل خود در هنگام اعتبار سنجی استفاده می کنیم.
دو روش استخراج ویژگی و انتخاب ویژگی را بررسی کردیم، در حالی که هر دو روش برای کاهش تعداد ویژگی های یک مجموعه داده استفاده می شود، ولی تفاوت مهمی بین آن ها وجود دارد. انتخاب ویژگی انتخاب و حذف ویژگی های داده شده بدون تغییر در آنها است و کاهش بعد ویژگی ها را به بعد پایین تر تبدیل می کند. مزایای مختلفی در انجام انتخاب ویژگی و کاهش ابعاد وجود دارد که شامل تفسیرپذیری مدل، به حداقل رساندن بیش از حد مناسب و همچنین کاهش اندازه مجموعه train و در نتیجه زمان train است.

