استخراج ویژگی یکی از مولفه های بسیار مهم در مبحث شناسایی الگو می باشد. در دنیای واقعی اغلب با هزاران و یا حتی صدها هزار ویژگی سروکار داریم که به دلایل زیادی مثل زمان بر بودن و هزینه بر بودن کار در فضا با ابعاد بالا می تواند نامطلوب باشد. کاهش ابعاد در زمینه هایی که با تعداد زیادی متغیر سرو کار دارند مانند پردازش سیگنال ، تشخیص گفتار ، نورفورماتیک و بیوانفورماتیک معمول است. به عنوان مثال هنگام کار با تصاویر، یک تصویر رنگی 256 × 256 پیکسل تبدیل به 196608 ویژگی میشود، که هر یک از این پیکسل ها می توانند یکی از 256 مقدار ممکن را بدست آورند، در نهایت 256196608 حالت مختلف می تواند باشد. خب این مسئله مشکل ساز است زیرا عملا ما قادر به جمع آوری تمام مشاهدات برای پوشش دهی بخش کوچکی از این حالات نخواهیم بود و الگوریتم های یادگیری ما اطلاعات کافی برای عملکرد صحیح را ندارند. برای کاهش ابعاد دو رویکرد انتخاب ویژگی و استخراج ویژگی داریم که در این بخش با استفاده از استخراج ویژگی را بررسی میکنیم که معمولاً به صورت خطی و غیرخطی تقسیم می شوند، جلوتر با روش های PCA، KernelPCA، LDA، NMF و TSVD آشنا خواهیم شد.
در کل همه ویژگی ها با هم برابر نیستند و هدف از استخراج ویژگی برای کاهش ابعاد این است که ویژگی ها جوری تغییر کنند که در انتها به مجموعه ی جدید Pnew ، که در آن Porginal بزرگتر از Pnew است برسیم در حالی که بسیاری از اطلاعات اساسی را حفظ می کنند. به عبارت دیگر، ما ویژگی ها را کاهش میدهیم ولی اطلاعاتی که آن ها برای پیش بینی با کیفیت دارند را تا حد زیادی حفظ می کنیم. حال میخواهیم، تعدادی از تکنیک های استخراج ویژگی را برای انجام این کار بررسی کنیم.
یک نکته در مورد تکنیک های استخراج ویژگی که در زیر بررسی می کنیم، این است که ویژگی های جدید توسط انسان قابل تفسیر نخواهند بود. ولی با آنها تا حد زیادی میتوانیم مدل هامون را آموزش دهیم، اما به عنوان مجموعه ای از اعداد تصادفی در چشم انسان ظاهر می شوند. اگر می خواستیم تفسیر مدل ها را توسط خودمون حفظ کنیم، کاهش ابعاد از طریق انتخاب ویژگی گزینه بهتری است.
کاهش ویژگی ها با استفاده از اجزای اصلی
چگونگی کاهش ویژگی ها با حفظ واریانس داده ها:
برای این کار از روش PCA استفاده می کنیم. PCA را از کتابخانه sklearn فراخوانی می کنیم.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
# Load libraries
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import datasets
# Load the data
digits = datasets.load_digits()
# Standardize the feature matrix
features = StandardScaler().fit_transform(digits.data)
# Create a PCA that will retain 99% of variance
pca = PCA(n_components=0.99, whiten=True)
# Conduct PCA
features_pca = pca.fit_transform(features)
# Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_pca.shape[1])
#output:
Original number of features: 64
Reduced number of features: 54
|
تحلیل مولفه اصلی Principal component analysis (PCA) یک روش محبوب کاهش خطی ابعاد است. تمرکز PCA بر روی اجزای اصلی ماتریس ویژگی ها می باشد که بیشترین واریانس را حفظ می کنند. PCA یک تکنیک بدون نظارت است، به این معنی که از اطلاعات بردار هدف استفاده نمی کند و فقط ماتریس ویژگی را در نظر می گیرد.
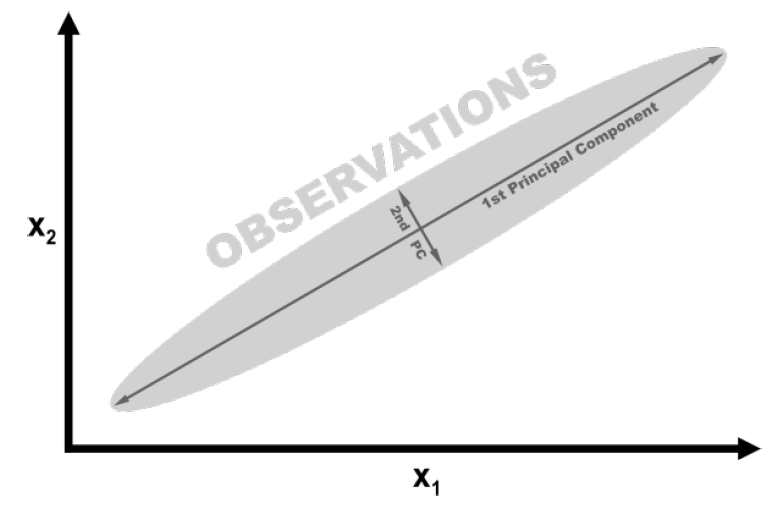
برای توصیف ریاضی نحوه عملکرد PCA، ما می توانیم با استفاده از یک مثال ساده و ملموس آن را شرح دهیم. در شکل زیر ، داده های ما شامل دو ویژگی x1 و x2 است که داده ها با طول زیاد و ارتفاع بسیار کم پخش می شوند. در واقع، می توان گفت که واریانس “طول” به طور قابل توجهی بیشتر از “ارتفاع” است جهت طول از اهمیت بیشتری نسبت به جهت ارتفاع برخوردار است. به جای طول و ارتفاع، ما به “جهت ” با بیشترین واریانس (مهم ترین) به عنوان اولین مولفه اصلی و “جهت ها” با کمترین واریس (کم اهمیت) به عنوان دومین مولفه اصلی اشاره می کنیم.
اگر بخواهیم ویژگی های خود را کاهش دهیم، یک راه این است که همه داده های فضای 2 بعدی خود را بر روی مولفه اصلی که یک بعدی است قرار دهیم. ما اطلاعات ذخیره شده در مولفه اصلی دوم را از دست خواهیم داد ، اما در برخی شرایط می تواند یک معامله قابل قبول باشد، این PCA است.
برای پیاده سازی PCA در کتابخانه scikit-learn از ابزار pca استفاده می شود.PCA چند تا پارامترمی گیرد اولی n_components است که بسته به مسئله به دو صورت مقداردهی می شود. اگرمقدری که می گیرد بیشتر از 1 باشد، اکثر ویژگی ها را برمی گرداند که در این صورت نمیتواند تعداد ویژگی هایی که بهینه است را برگرداند. اگر آرگومان n_components بین 0 تا 1 باشد ، pca حداقل مقدار ویژگی هایی را که این اختلاف را حفظ می کند، برمی گرداند. معمولاً از مقادیر 0.95 و 0.99 استفاده می شود، به این معنی که 95٪ یا 99٪ از واریانس ویژگیهای اصلی حفظ شده است.پارامتر بعدی whiten = True مقادیر هر مولفه اصلی را به گونه ای تغییر می دهد که دارای واریانس واحد و میانگین صفر باشند. پارامتردیگر “svd_solver=”randomized است، که یک الگوریتم تصادفی به منظور یافتن اولین مولفه های اصلی در کمترین زمان ممکن است.
خروجی نشان می دهد که PCA به ما اجازه می دهد که ابعاد مسئله مان را با 10 ویژگی کاهش دهیم در حالی که 99٪ اطلاعات (واریانس) ماتریس ویژگی را حفظ کرده ایم.
کاهش ویژگی وقتی داده ها به طور خطی تفکیک نشوند
چگونگی کاهش ابعاد وقتی داده هامون جداپذیر خطی نیستند:
یک مدل توسعه یافته ی PCA است که از kernel برای کاهش بعد غیر خطی استفاده می کند:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# Load libraries
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
# Create linearly inseparable data
features, _ = make_circles(n_samples=1000, random_state=1, noise=0.1, factor=0.1)
# Apply kernal PCA with radius basis function (RBF) kernel
kpca = KernelPCA(kernel="rbf", gamma=15, n_components=1)
features_kpca = kpca.fit_transform(features)
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kpca.shape[1])
#output:
Original number of features: 2
Reduced number of features: 1
|
در کل PCA قادر است ابعاد ماتریس ویژگی ما را کاهش دهد. PCA استاندارد از روش خطی برای کاهش ویژگی استفاده می کند. اگر داده ها به صورت خطی قابل تفکیک باشند یعنی وقتی می توانید بین کلاس های مختلف یک خط مستقیم ترسیم کنید، PCA به خوبی کار می کند. در حالی که، اگر داده ها به صورت خطی قابل جداشدن نباشند ( فقط با استفاده از مرز به صورت منحنی می توانید کلاس ها را جدا کنید)، تغییر شکل خطی کارایی نخواهد داشت. در روش بالا از کتابخانه scikit-learn با استفاده متد make_circles یک مجموعه داده برای تولید یک بردار هدف دو کلاسه و دو ویژگی شبیه سازی شده است . make_circles داده ها را به صورت خطی از هم جدا نمی کند. نشان می دهد که یک کلاس از هر طرف توسط کلاس دیگر احاطه شده است.
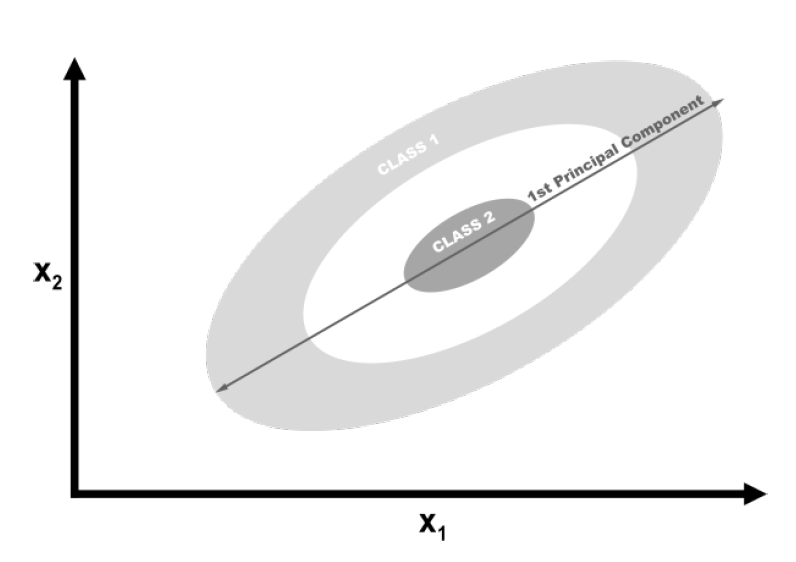
اگر ما از PCA خطی برای کاهش ابعاد داده های خود استفاده می کردیم ، این دو کلاس به صورت خطی روی اولین مولفه اصلی پرتاب می شوند، به گونه ای که در هم می آمیزند.
در حالت ایده آل، ما می خواهیم انتقالی را ایجاد کنیم که هم ابعاد را کاهش دهد و هم داده ها را به صورت خطی قابل تفکیک کند. Kernel PCA می تواند هر دو را انجام دهد.
kernel ها به ما این امکان را می دهند که داده هایی که به صورت خطی جدایی ناپذیر هستند را در ابعاد بالاتر که قابل تفکیک خطی است، انتقال دهیم. این ترفند را Kernel می نامند. در کل به زبان ساده تر به Kernel ها به عنوان روش های مختلف انتقال یا فرافکنی داده ها نگاه کنید. برای پیلده سازی تعدادی Kernel در کتابخانه scikit-learn به نام kernelPCA وجود دارد که می توانیم از آنها استفاده کنیم. یکی از Kernel های معروف rbf (radial basis function) گوسین است، اما انواع دیگر Kernel عبارتند از چند جمله ای polynomial kernel (poly) و sigmoid kernel (sigmoid). حتی می توانیم یک انتقال خطی را مشخص کنیم که همان نتایج PCA استاندارد را ایجاد می کند.
یکی از نقاط ضعف Kernel PCA این است که تعدادی پارامتر دارد که باید آنها را مشخص کنیم. به عنوان مثال، در قطعه کد قبل n_components را روی 0.99 تنظیم کردیم تا PCA ویژگی ها را با حفظ 99٪ واریانس انتخاب کند. ما این پارامتر را در Kernel PCA نداریم به جای آن باید تعدادی پارامتر تعریف کنیم. از طریق آزمون و خطا می توان مقادیر این پارامتر ها را تعیین کرد به طور کلی ما می توانیم چندین بار مدل یادگیری ماشین خود را آموزش دهیم هر بار با یک Kernel یا مقادیر متفاوت پارامتر. هنگامی که ترکیبی را پیدا کنیم که بالاترین کیفیت مقادیر پیش بینی شده را به ما بدهد، کار ما تمام می شود.
کاهش ویژگی با به حداکثر رساندن تفکیک کلاس
چگونگی کاهش ویژگی مورد استفاده در مرحله پیش پردازش برای طبقه بندی یک الگو:
linear discriminant analysis یا تجزیه و تحلیل تفکیک خطی (LDA) می تواند ویژگی ها را بر روی محورهای مولفه قرار دهد به طوری که تفکیک کلاس ها را به حداکثر برساند:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
# Load libraries
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# Load Iris flower dataset:
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Create and run an LDA, then use it to transform the features
lda = LinearDiscriminantAnalysis(n_components=1)
features_lda = lda.fit(features, target).transform(features)
# Print the number of features
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_lda.shape[1])
#output:
Original number of features: 4
Reduced number of features: 1
|
می توانیم از _explained_variance_ratio برای مشاهده میزان واریانس توسط هر یک از مولفه ها استفاده کنیم. در این جا، تک مولفه ما بیش از 99٪ از واریانس را نشان میدهد:
|
1
2
3
4
5
|
lda.explained_variance_ratio_
#output:
array([ 0.99147248])
|
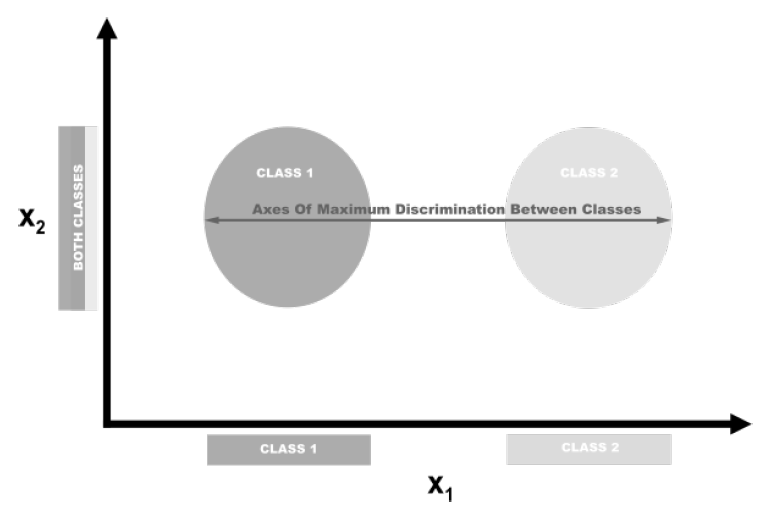
LDA یک الگوی طبقه بندی و همچنین یک روش محبوب برای کاهش ابعاد است. LDA از این نظر که ویژگی ها را بر روی فضایی با بعد پایین تر می برد، مشابه PCA کار می کند. ولی، PCA فقط به محورهای مولفه ها توجه می کند که واریانس داده ها را به حداکثر می رساند، در حالی که در LDA هدف دیگر به حداکثر رساندن اختلافات بین کلاس ها است. در مثال زیر، ما داده هایی داریم که شامل دو کلاس هدف و دو ویژگی هستند. اگر داده ها را بر روی محور y قرار دهیم، این دو کلاس به راحتی قابل تفکیک نیستند (یعنی همپوشانی دارند)، ولی اگر داده ها را بر روی محور x قرار دهیم ، بردار ویژگی برای ما باقی می ماند و همین طور کلاس ها تفکیک پذیرند. قطعا در دنیای واقعی رابطه بین کلاس ها پیچیده تر و ابعاد خیلی بیشتر خواهد بود، اما مفهوم به همین شکل است.
برای پیاده سازی LDA از کتابخانه scikit-learn، ابزار LinearDiscriminantAnalysis را فراخوانی می کنیم که شامل یک پارامتر n_components است، که تعداد ویژگی هایی را که می خواهیم برگردانده شود را نشان می دهد. برای فهمیدن اینکه چه مقداری برای n_components استفاده شود، می توانیم از این _explained_variance_ratio استفاده کنیم که واریانس توسط هر ویژگی خروجی را نشان می دهد و یک آرایه مرتب شده است. مثلا:
|
1
2
3
4
|
lda.explained_variance_ratio_
#output:
array([ 0.99147248])
|
معمولا، می توانیم LinearDiscriminantAnalysis را با n_components تنظیم شده بر روی None اجرا کنیم تا نسبت واریانس توسط هر ویژگی را بازگردانیم، سپس محاسبه کنیم چند مولفه نیاز است که بالاتر از آستانه واریانس به دست بیاوریم (اغلب 0.95 یا 0.99):
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
# Create and run LDA
lda = LinearDiscriminantAnalysis(n_components=None)
features_lda = lda.fit(features, target)
# Create array of explained variance ratios
lda_var_ratios = lda.explained_variance_ratio_
# Create function
def select_n_components(var_ratio, goal_var: float) -> int:
# Set initial variance explained so far
total_variance = 0.0
# Set initial number of features
n_components = 0
# For the explained variance of each feature:
for explained_variance in var_ratio:
# Add the explained variance to the total
total_variance += explained_variance
# Add one to the number of components
n_components += 1
# If we reach our goal level of explained variance
if total_variance >= goal_var:
# End the loop
break
# Return the number of components
return n_components
# Run function
select_n_components(lda_var_ratios, 0.95)
|
کاهش ویژگی ها با استفاده از ضریب ماتریس
چگونگی کاهش ویژگی توسط ماتریس ویژگی مقادیر غیر منفی (NMF):
برای کاهش ابعاد ماتریس ویژگی میتوانیم از non-negative matrix factorization یا ضریب ماتریس غیر منفی (NMF) استفاده کنید:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
# Load libraries
from sklearn.decomposition import NMF
from sklearn import datasets
# Load the data
digits = datasets.load_digits()
# Load feature matrix
features = digits.data
# Create, fit, and apply NMF
nmf = NMF(n_components=10, random_state=1)
features_nmf = nmf.fit_transform(features)
# Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_nmf.shape[1])
#output:
Original number of features: 64
Reduced number of features: 10
|
NMF یک تکنیک بدون نظارت برای کاهش ابعاد خطی است که ماتریس ویژگی را به ماتریس هایی تبدیل می کند که رابطه نهفته بین مقادیر و ویژگی های آنها را فاکتور می کند (مثلا یک ماتریس ویژگی به چندین ماتریس تقسیم می شود که محصول آنها ماتریس اصلی را تقریب می زند). پس، NMF می تواند ابعاد را کاهش دهد زیرا در ضرب ماتریس، دو عامل (ماتریس هایی که ضرب می شوند) می توانند ابعاد خیلی کمتری نسبت به ماتریس اصلی داشته باشند. به طور کلی، با توجه به تعداد مشخصی از ویژگی های برگشتی(r)، NMF ماتریس ویژگی را فاکتور می کند، به این ترتیب:
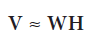
V ماتریس ویژگی است که از حاصل ضرب d × n به دست می آید ( d ویژگی ها ، n مشاهدات یا مقادیر ویژگی هامون) ، W ماتریس حاصل ضرب d × r است و H ماتریس حاصل ضرب r × n است. با تنظیم مقدار r می توان میزان کاهش ابعاد مورد نظر را به دست آورد.
یکی از ویژگی های اصلی NMA این است که، ماتریس ویژگی نمی تواند حاوی مقادیر منفی باشد. علاوه بر این، برخلاف PCA و سایر تکنیک هایی که بررسی کرده ایم، NMA واریانس توضیح داده شده از ویژگی های خروجی را به ما ارائه نمی دهد. بنابراین، بهترین راه برای یافتن مقدار مطلوب n_components این است که طیف وسیعی از مقادیر را پیدا کنیم تا در مدل نهایی ما بهترین نتیجه را پیدا کند.
کاهش ویژگی ها در داده های پراکنده
چگونگی کاهش ابعاد ویژگی وقتی یک ماتریس ویژگی پراکنده داریم:
میتوانیم از روش Truncated Singular Value Decomposition (TSVD) استفاده کنیم.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
# Load libraries
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import TruncatedSVD
from scipy.sparse import csr_matrix
from sklearn import datasets
import numpy as np
# Load the data
digits = datasets.load_digits()
# Standardize feature matrix
features = StandardScaler().fit_transform(digits.data)
# Make sparse matrix
features_sparse = csr_matrix(features)
# Create a TSVD
tsvd = TruncatedSVD(n_components=10)
# Conduct TSVD on sparse matrix
features_sparse_tsvd = tsvd.fit(features_sparse).transform(features_sparse)
# Show results
print("Original number of features:", features_sparse.shape[1])
print('"Reduced number of features:", features_sparse_tsvd.shape[1])
#output:
Original number of features: 64
Reduced number of features: 10
|
TSVD مشابه PCA است ولی PCA در اغلب موارد در یکی از مراحل خود از SVD استفاده می کند. در SVD معمولی، وقتی d تعداد ویژگی ها باشد، ماتریس های عاملی ایجاد می کند که d × d هستند، در حالی که TSVD فاکتورهایی را برمی گرداند که n × n هستند، جایی که n قبلاً توسط یک پارامتر مشخص شده است. مزیت عملی TSVD این است که بر خلاف PCA، روی ماتریس های ویژگی پراکنده کار می کند. چیزی که در مورد TSVD وجود دارد این است که به دلیل استفاده از یک عدد تصادفی، خروجی می توان n بار ما بین fitting لوپ شود. یک روش راحت این است که از fit فقط یک بار در خط پیش پردازش استفاده شود، سپس چندین بار transform به کار گرفته شود.
همانند LDA، باید تعداد ویژگی موردنظر را برای خروجی مشخص کنیم. این کار با پارامتر n_components انجام می شود. خب سوالی که پیش می آید این است که مقدار بهینه component چند است؟ خب یک روش برای بهینه سازی به عنوان یک ابر پارامتر در طول انتخاب مدل است (مقداری را برای n_components انتخاب کنید که بهترین مقدار برای آموزش مدل باشد). از آنجا که TSVD نسبت واریانس ماتریس ویژگی اصلی را توسط هر مولفه فراهم می کند، می توانیم تعداد مولفه هایی را انتخاب کنیم که مقدار واریانس مورد نظر را توضیح می دهند (95٪ یا 99٪ مقادیر مشترک هستند) به عنوان مثال، در زیر سه مولفه اول خروجی تقریباً 30٪ از واریانس داده های اصلی را توضیح می دهند:
|
1
2
3
4
5
|
# Sum of first three components' explained variance ratios
tsvd.explained_variance_ratio_[0:3].sum()
#output:
0.30039385386597783
|
می توانیم روند را به صورت خودکار با ایجاد یک تابع که TSVD را با n_components روی یکی کمتر از تعداد ویژگی های اصلی تنظیم شده اجرا کنیم و سپس تعداد مولفه هایی را که مقدار دلخواه واریانس داده اصلی را توضیح می دهند محاسبه کنید:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
# Create and run an TSVD with one less than number of features
tsvd = TruncatedSVD(n_components=features_sparse.shape[1]-1)
features_tsvd = tsvd.fit(features)
# List of explained variances
tsvd_var_ratios = tsvd.explained_variance_ratio_
# Create a function
def select_n_components(var_ratio, goal_var):
# Set initial variance explained so far
total_variance = 0.0
# Set initial number of features
n_components = 0
# For the explained variance of each feature:
for explained_variance in var_ratio:
# Add the explained variance to the total
total_variance += explained_variance
# Add one to the number of components
n_components += 1
# If we reach our goal level of explained variance
if total_variance >= goal_var:
# End the loop
break
# Return the number of components
return n_components
# Run function
select_n_components(tsvd_var_ratios, 0.95)
|
تا این جا انواع روش های کاهش ابعاد با استفاده از استخراج ویژگی را با هم بررسی کردیم. یک نتیجه گیری کلی در این مبحث این بود که کاهش ابعاد با استفاده از استخراج ویژگی فضای ویژگی جدیدی است که در آن ویژگی های اصلی نشان داده می شوند و فضای جدید از بعد کمتری نسبت به فضای اصلی برخوردار است.
خیلی عالی و مفید بود ممنون