چگونه با استفاده از بهینه سازها ، شبکه عصبی را سریعتر آموزش دهیم؟

بهینه سازی الگوریتم های یادگیری ماشین

بهینه سازی (Optimization) فرآیندی برای جستجوی پارامترهایی است که توابع ما را به حداقل یا حداکثر می رساند. وقتی مدل یادگیری ماشین را آموزش می دهیم ، معمولاً از بهینه سازی غیرمستقیم استفاده می کنیم. ما یک معیار خاص را انتخاب می کنیم – مانند دقت یا صحت – که نشان می دهد مدل ما چقدر خوب می تواند مسئله را حل کند. با این حال ، ما یک تابع هزینه J (θ) را نیز بهینه می کنیم و امیدواریم که به حداقل رساندن مقدار آن ، معیار مورد نظر ما را بهبود بخشد. البته انتخاب تابع هزینه معمولاً به مسئله ای که هدف ما حل آن است مربوط می شود.

تله های بین راه

معلوم است که اغلب یافتن حداقل توابع هزینه غیر محدب کار ساده ای نیست ، و ما مجبوریم از استراتژی های پیشرفته بهینه سازی برای تعیین مکان آنها استفاده کنیم. اگر حساب دیفرانسیل را یاد گرفته باشید ، مطمئناً مفهوم حداقل محلی را می دانید – اینها بزرگترین تله هایی هستند که بهینه ساز ما می تواند در آنها گیر کند. برای کسانی که هنوز به این بخش شگفت انگیز از ریاضیات برخورد نکرده اند ، فقط می گویم که این نقاط، نقاطی هستند که تابع حداقل مقدار را می گیرد ، اما فقط در یک منطقه خاص. نمونه ای از چنین وضعیتی در سمت چپ شکل زیر نشان داده شده است. به وضوح می توان دریافت که نقطه واقع شده توسط بهینه ساز در کل بهینه ترین راه حل نیست.
نقاط زینی (sadle points) چالش برانگیزتر تلقی می شوند. اینها سطح مسطح هستند ، جایی که مقدار تابع هزینه تقریباً ثابت است. این وضعیت در سمت راست همان شکل نشان داده شده است. در این نقاط شیب تقریباً از همه جهات صفر است و فرار را غیرممکن می کند.
گاهی اوقات ، به خصوص در مورد شبکه های چند لایه ، ممکن است به مناطقی برخورد کنیم که شیب تابع هزینه به شدت افزایش می یابد، که منجر به برداشتن گام های بزرگ می شود و اغلب کل بهینه سازی قبلی را خراب می کند. با این حال ، با برش گرادیان – تعریف حداکثر مقدار شیب مجاز ، می توان به راحتی از این مشکل جلوگیری کرد.

گرادیان کاهشی

قبل از اینکه با الگوریتم های پیشرفته تری آشنا شویم ، بیایید نگاهی به برخی از استراتژی های پایه بیندازیم. احتمالاً یکی از ساده ترین رویکردها این است که به سادگی در جهت مخالف شیب حرکت کنید. این استراتژی را می توان با معادله زیر توصیف کرد.

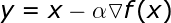
پارامتر α نرخ یادگیری است ، که به اندازه گام در هر تکرار گفته می شود . انتخاب آن به سرعت یادگیری و دقت نتیجه بستگی دارد. انتخاب گام کوچک ما را به محاسبات خسته کننده و ضرورت انجام تکرارهای بسیار بیشتر می رساند. از طرف دیگر ، انتخاب مقدار بسیار بالا می تواند مانع از یافتن حداقل شود. چنین وضعیتی در شکل 2 ارائه شده است – ما می توانیم ببینیم که چگونه در تکرارهای بعدی به عقب باز می گردیم و قادر به یافتن نقطه مینیمم نیستیم. در همین حال ، مدلی که در آن گام مناسب تعریف شده بود ، تقریباً بلافاصله حداقل یافت می شود.

علاوه بر این ، این الگوریتم نسبت به مشکلات مربوط به نقاط زینی آسیب پذیر است. از آنجا که اندازه تصحیح انجام شده در تکرارهای بعدی متناسب با شیب محاسبه شده است ، ما قادر به فرار از سطح صاف نخواهیم بود.
درآخر ، این کار نیاز به استفاده از کل داده آموزش در هر تکرار دارد. این بدان معنی است که برای انجام مرحله بهینه سازی بعدی ، باید در هر تکرار به همه داده ها نگاه کنیم. وقتی مجموعه آموزشی شامل چندین هزار مثال باشد، تصور کنید که در هر تکرار از کل مجموعه استفاده کنیم. این کار باعث اتلاف وقت و حافظه کامپیوتر می شود. همه این عوامل باعث می شود که گرادیان کاهشی ، در ساده ترین شکل خود ، در اکثر موارد کارساز نباشد.