رگرسیون خطی

تحلیل رگرسیون از مجموعه ای از روش های یادگیری ماشین تشکیل شده است که برای پیش بینی یک مقدار پیوسته از مدل های رگرسیون استفاده می شود. پیش بینی قیمت های خانه با توجه به ویژگی های خانه مانند اندازه ، قیمت و غیره یکی از نمونه های متداول رگرسیون است. این یک تکنیک با نظارت است. رگرسیون خطی یکی از ساده ترین الگوریتم های یادگیری با نظارت در مجموعه ابزارها می باشد. اگر تا به حال یک دوره مقدماتی آماری در دانشگاه گذرانده اید، احتمالاً آخرین موضوعی که شما پوشش داده اند رگرسیون خطی بوده است. در واقع، آنقدر ساده است که گاهی اوقات اصلاً یادگیری ماشین در نظر گرفته نمی شود! واقعیت این است که رگرسیون خطی وقتی که بردار هدف مقدار کمی است (مثل قیمت مسکن، سن) یک روش معمول و مفید برای پیش بینی است. در این بخش انواع روش های رگرسیون خطی برای ایجاد مدل های پیش بینی با عملکرد خوب را پوشش خواهیم داد.

fit کردن یک خط

چگونگی آموزش یک مدل که نشان دهنده یک رابطه خطی بین ویژگی و بردار هدف باشد:

از یک رگرسیون خطی استفاده می کنیم (درscikit-learn، LinearRegression).

# Load libraries
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston

# Load data with only two features
boston = load_boston()
features = boston.data[:,0:2]
target = boston.target

# Create linear regression
regression = LinearRegression()

# Fit the linear regression
model = regression.fit(features, target)

رگرسیون خطی فرض می کند که رابطه بین ویژگی ها و بردار هدف تقریباً خطی است. یعنی تأثیر effect (ضریب coefficient، وزن weight یا پارامتر parameter نامیده میشود) ویژگی ها بر روی بردار هدف ثابت است. در این مسئله، به منظور توضیح، مدل خود را فقط با استفاده از دو ویژگی آموزش داده ایم. این بدان معنی است که مدل خطی ما:

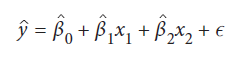
ŷ هدف است، x_i داده های یک ویژگی واحد است، β₁ و β₂ ضرایبی هستند که با fit شدن مدل مشخص می شوند و ϵ خطا است. بعد از اینکه مدل خود را fit کردیم، می توانیم مقدار هر پارامتر را مشاهده کنیم. به عنوان مثال، β₀، که bias یا intercept نیز نامیده می شود، با استفاده از intercept_ قابل مشاهده است:

# View the intercept
model.intercept_

22.46681692105723

و β₁ و β₂ با استفاده از coef_ نشان داده شده است:

# View the feature coefficients
model.coef_

array([-0.34977589, 0.11642402])

در دیتاست مسئله ما، هدف  مقدار میانه و متوسط ارزش خانه بوستون (در دهه 1970) به هزار دلار است. بنابراین قیمت خانه اول در مجموعه داده:

# First value in the target vector multiplied by 1000
target[0]*1000

24000.0

با استفاده از روش predict می توان مقداری را برای آن خانه پیش بینی کرد:

# Predict the target value of the first observation, multiplied by 1000
model.predict(features)[0]*1000

24560.23872370844

تقریبا بد نیست! مدل ما فقط 560.24 دلار بیشتر بود!

مزیت عمده رگرسیون خطی تا حد زیادی تفسیرپذیری آن است، زیرا ضرایب مدل تأثیر یک واحد تغییر بر روی بردار هدف است. به عنوان مثال، اولین ویژگی در راه حل ما تعداد جرایم به ازای هر ساکن است. ضریب مدل ما از این ویژگی تقریبا 0.35- بود ، به این معنی که اگر این ضریب را در 1000 ضرب کنیم (از آنجا که بردار هدف قیمت خانه در هزار دلار است)، برای هر سرانه یک جرم اضافی تغییر قیمت خانه داریم:

# First coefficient multiplied by 1000
model.coef_[0]*1000

-349.77588707748947

این می گوید که به طور سرانه هر جرم قیمت خانه را تقریباً 350 دلار کاهش می دهد!

مدیریت اثرات تعاملی

چگونگی وابستگی تأثیر یک ویژگی بر متغیر هدف به ویژگی دیگر:

برای به دست آوردن این وابستگی با استفاده از ویژگی های چند جمله ای Polynomial Features در scikit learn ایجاد می کنیم.

# Load libraries
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.preprocessing import PolynomialFeatures

# Load data with only two features
boston = load_boston()
features = boston.data[:,0:2]
target = boston.target

# Create interaction term
interaction = PolynomialFeatures(
degree=3, include_bias=False, interaction_only=True)
features_interaction = interaction.fit_transform(features)

# Create linear regression
regression = LinearRegression()

# Fit the linear regression
model = regression.fit(features_interaction, target)

گاهی اوقات تأثیر یک ویژگی بر متغیر هدف ما حداقل تا حدی به ویژگی دیگری وابسته است. یک مثال ساده مبتنی بر قهوه را تصور کنید که در آن ما دو ویژگی دودویی داریم – وجود قند (sugar) و اینکه آیا هم زده ایم یا هم نزده ایم (stirred) و ما می خواهیم شیرین بودن قهوه را پیش بینی کنیم. فقط گذاشتن شکر در قهوه (sugar=1, stirred=0) طعم قهوه را شیرین نخواهد کرد (تمام شکر در پایین آن است!) و فقط قهوه را بدون افزودن شکر هم بزنید (sugar=0, stirred=1) آن را شیرین نیز نخواهد کرد. در عوض این تعامل قرار دادن شکر در قهوه و هم زدن قهوه (sugar=1, stirred=1) است که باعث طعم شیرین قهوه می شود. اثرات شکر و هم زدن بر روی شیرینی به یکدیگر وابسته هستند. در این حالت می گوییم اثر متقابل بین ویژگی های sugar و stirred وجود دارد.

ما می توانیم با درج ویژگی جدیدی که شامل محصول مقادیر متناظر از ویژگیهای متقابل است، اثرات متقابل را حساب کنیم:

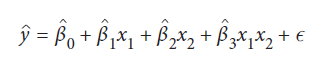
x₁ و x₂ به ترتیب مقادیر sugar و stirred هستند و x₁x₂ نشان دهنده تعامل بین این دو است.

در این مسئله، ما از یک مجموعه داده استفاده کردیم که فقط شامل دو ویژگی است. در اینجا اولین مقادیر مشاهده برای هر یک از این ویژگی ها است:

# View the feature values for first observation
features[0]

array([ 6.32000000e-03, 1.80000000e+01])

برای ایجاد اصطلاح تعامل، ما به راحتی برای هر مشاهده آن دو مقدار را با هم ضرب می کنیم:

# Import library
import numpy as np

# For each observation, multiply the values of the first and second feature
interaction_term = np.multiply(features[:, 0], features[:, 1])

سپس می توانیم اصطلاح تعامل را برای اولین مشاهده ببینیم:

# View interaction term for first observation
interaction_term[0]

0.11376

اگرچه اغلب ما یک دلیل اساسی برای این باور داریم که تعاملی بین دو ویژگی وجود دارد، اما گاهی اوقات چنین نمی کنیم. در این موارد استفاده از  PolynomialFeaturesدر scikit-learn برای ایجاد اصطلاحات تعامل برای همه ترکیبات ویژگی می تواند مفید باشد. سپس می توانیم از استراتژی های انتخاب مدل برای شناسایی ترکیبی از ویژگی ها و اصطلاحات تعامل که بهترین مدل را تولید می کنند، استفاده کنیم.

برای ایجاد اصطلاحات تعامل با استفاده از ویژگی های چند جمله ای (PolynomialFeatures)، سه پارامتر مهم وجود دارد که باید تنظیم کنیم. مهمترین، interaction_only = True به PolynomialFeatures می گوید که فقط اصطلاحات تعامل را برگرداند (و نه ویژگی های چند جمله ای ، که در بخش بعدی به آن خواهیم پرداخت). به طور پیش فرض، Polynomial Features به شما یک ویژگی اضافه می کند که به آن bias می گویند. ما می توانیم با include_bias = False از این امر جلوگیری کنیم. سرانجام، پارامتر degree حداکثر تعداد ویژگی ها را برای ایجاد اصطلاحات تعامل تعیین می کند (درصورتی که بخواهیم یک اصطلاح تعامل ایجاد کنیم که ترکیبی از سه ویژگی باشد). با بررسی اینکه آیا مقادیر ویژگی مشاهده اول و مقدار اصطلاح تعامل با نسخه محاسبه دستی ما مطابقت دارد، می توانیم خروجی PolynomialFeatures را از راه حل خود ببینیم:

# View the values of the first observation
features_interaction[0]

array([ 6.32000000e-03, 1.80000000e+01, 1.13760000e-01])

fit کردن یک رابطه غیرخطی

چگونگی مدل کردن یک رابطه غیرخطی:

با گنجاندن ویژگی های چند جمله ای در مدل رگرسیون خطی، یک رگرسیون چند جمله ای ایجاد می کنیم.

# Load library
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.preprocessing import PolynomialFeatures

# Load data with one feature
boston = load_boston()
features = boston.data[:,0:1]
target = boston.target

# Create polynomial features x^2 and x^3
polynomial = PolynomialFeatures(degree=3, include_bias=False)
features_polynomial = polynomial.fit_transform(features)

# Create linear regression
regression = LinearRegression()

# Fit the linear regression
model = regression.fit(features_polynomial, target)

تا اینجا فقط در مورد مدل سازی روابط خطی بحث کردیم. یک مثال از یک رابطه خطی مانند ساختمان و ارتفاع ساختمان است. در رگرسیون خطی، یعنی یک ساختمان 20 طبقه تقریباً دو برابر یک ساختمان 10 طبقه، که تقریباً دو برابر ساختمان 5 طبقه خواهد بود،. با این حال، بسیاری از روابط خطی نیستند.

وقتی می خواهیم یک رابطه غیرخطی را مدل کنیم، به عنوان مثال، رابطه بین تعداد ساعاتی که دانشجو می خواند و نمره ای که او در آزمون کسب می کند. می توان تصور کرد که بین دانش آموزانی که به مدت یک ساعت مطالعه می کنند تفاوت زیادی در نمره آزمون نسبت به دانشجویانی که اصلاً مطالعه نکرده اند وجود دارد. با این وجود، تفاوت بسیار کمتری در نمرات آزمون بین دانشجویی که 99 ساعت درس خوانده است و دانش آموزی که 100 ساعت درس خوانده است، وجود دارد. تأثیری که یک ساعت مطالعه روی نمره آزمون دانش آموز دارد با افزایش تعداد ساعت کاهش می یابد.

رگرسیون چند جمله ای مدل پبشرفته رگرسیون خطی است که به ما اجازه می دهد روابط غیرخطی را مدل کنیم. برای ایجاد یک رگرسیون چند جمله ای، تابع خطی را که قسمت اول این بخش استفاده کردیم را تبدیل می کنیم:

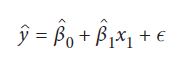
با افزودن ویژگی های چند جمله ای به یک عملکرد چند جمله ای تبدیل می شود:

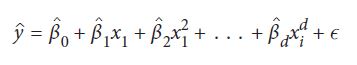
در فرمول بالا d درجه چند جمله ای است. حالا چطور می توانیم از یک رگرسیون خطی برای یک تابع غیرخطی استفاده کنیم؟ پاسخ این است که چگونگی fit شدن رگرسیون خطی با مدل مون را تغییر نمی دهیم، بلکه فقط ویژگی های چند جمله ای را اضافه می کنیم. یعنی، رگرسیون خطی “نمی داند” که x² یک تغییر درجه دوم x است. فقط آن را یک متغیر دیگر می داند.

شرح عملی تر به ترتیب زیر خواهد بود. برای مدل سازی روابط غیرخطی، می توانیم ویژگی های جدیدی ایجاد کنیم که یک ویژگی موجود x، تا حدی قدرت x² ، x_³ و غیره را افزایش می دهد. هرچه تعداد بیشتری از این ویژگی های جدید اضافه کنیم، باعث انعطاف پذیر تر بودن “خط” ایجاد شده توسط مدل مون می شود. برای بهتر درک کردن تصور کنید که می خواهیم چند جمله ای درجه سه بسازیم. به منظور سادگی، ما فقط روی داده ی (اولین داده در مجموعه دیتاست) x₀ تمرکز خواهیم کرد:

# View first observation
features[0]

array([ 0.00632])

برای ایجاد یک ویژگی چند جمله ای، مقدار داده اول را به درجه دوم، x₁² می رسانیم:

# View first observation raised to the second power, x^2
features[0]**2

array([ 3.99424000e-05])

این ویژگی جدید ما خواهد بود. سپس اولین داده را نیز به درجه سوم، x₁³ می رسانیم:

# View first observation raised to the third power, x^3
features[0]**3

array([ 2.52435968e-07])

با قرار دادن هر سه ویژگی (x² ، x و x³) در ماتریس ویژگی های خود و سپس اجرای یک رگرسیون خطی، یک رگرسیون چند جمله ای انجام داده ایم:

# View the first observation's values for x, x^2, and x^3
features_polynomial[0]

array([ 6.32000000e-03, 3.99424000e-05, 2.52435968e-07])

ویژگی های چند جمله ای دارای دو پارامتر مهم هستند. اول، degree حداکثر درجه را برای ویژگی های چند جمله ای تعیین می کند. به عنوان مثال، degree=3 باشد x2 و x3 را تولید می کند. در آخر،  به طور پیش فرض PolynomialFeatures شامل یک ویژگی است (bias  نامیده می شود). با تنظیم include_bias = False می توانیم آن را هم حذف کنیم.

 

کاهش واریانس با تنظیم کننده (Regularization):

چگونگی کاهش  واریانس مدل رگرسیون خطی خود را کاهش دهید:

از یک الگوریتم یادگیری استفاده می کنیم که شامل shrinkage penalty باشد (تنظیم کننده هم نامیده می شود) مانند رگرسیون خط الراس ridge regression و رگرسیون لاسو lasso regression:

# Load libraries
from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

# Load data
boston = load_boston()
features = boston.data
target = boston.target

# Standardize features
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)

# Create ridge regression with an alpha value
regression = Ridge(alpha=0.5)

# Fit the linear regression
model = regression.fit(features_standardized, target)

در رگرسیون خطی استاندارد، مدل train می شود تا مجموع خطای مربع بین مقادیر واقعی (y_i) و پیش بینی، (y_i) مقادیر هدف یا مجموع مربع باقیمانده (RSS) را به حداقل برساند:

یادگیرنده های رگرسیون تنظیم کننده مشابه هستند، با این تفاوت که آنها سعی می کنند RSS و برخی از قانون تنظیم ها را برای اندازه کل مقادیر ضریب به حداقل برسانند، که shrinkage penalty  نامیده می شود زیرا سعی در کوچک کردن (shrink) مدل دارد. دو نوع متداول برای تنظیم کننده برای رگرسیون خطی وجود دارد: رگرسیون ridge و lasso. تنها تفاوت آنها در نوع shrinkage penalty می باشد. در رگرسیون ridge، shrinkage penalty  یک ابر پارامتر تنظیم است که ضربدر مجموع مربع همه ضرایب می شود:

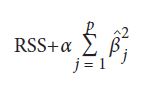
در فرمول بالا β_j ضریب j ام از ویژگی های p است و α یک ابر پارامتر است (مبحث بعدی). lasso مشابه همین است، فقط shrinkage penalty یک ابر پارامتر تنظیم کننده است که در مجموع مقدار مطلق تمام ضرایب ضرب می شود:

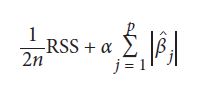
در فرمول بالا n تعداد داده ها است. بنابراین از کدام یک باید استفاده کنیم؟

 به عنوان یک قاعده کلی، رگرسیون ridge اغلب پیش بینی های بهتری از lasso تولید می کند، اما lasso (به دلایلی که در قسمت بعد توضیح خواهیم داد)  مدل های تفسیری بیشتری تولید می کند. اگر می خواهیم تعادل بین توابع penalty  رگرسیون ridge و lasso وجود داشته باشد، می توانیم از elastic net استفاده کنیم که به سادگی یک مدل رگرسیون با هر دو penalty  است. صرف نظر از اینکه از کدام یک استفاده می کنیم، رگرسیون های ridge و lasso می توانند مدل های بزرگ یا پیچیده را با درج مقادیر ضریب در تابع هزینه که سعی در به حداقل رساندن آن داریم، خطا را بالا ببرند.

ابر پارامتر α ، به ما اجازه می دهد که ضرایب را خطا را کنترل کنیم،  مقادیر بالاتر α باعث ایجاد مدل های ساده تر می شود. مقدار ایده آل α باید مانند هر ابر پارامتر دیگر تنظیم شود. در scikit-learn ، α با استفاده از پارامتر alpha تنظیم می شود.

scikit-learn شامل یک روش RidgeCV است که به ما امکان می دهد مقدار ایده آل را برای α انتخاب کنیم:

# Load library
from sklearn.linear_model import RidgeCV

# Create ridge regression with three alpha values
regr_cv = RidgeCV(alphas=[0.1, 1.0, 10.0])

# Fit the linear regression
model_cv = regr_cv.fit(features_standardized, target)

# View coefficients
model_cv.coef_


array([-0.91215884, 1.0658758 , 0.11942614, 0.68558782, -2.03231631,
2.67922108, 0.01477326, -3.0777265 , 2.58814315, -2.00973173,
-2.05390717, 0.85614763, -3.73565106])

سپس می توانیم مقدار α بهترین مدل را به راحتی مشاهده کنیم:

# View alpha
model_cv.alpha_

1.0

نکته آخر: چون در رگرسیون خطی مقدار ضرایب تا حدی با مقیاس ویژگی تعیین می شود و در مدل های تنظیم کننده همه ضرایب با هم جمع می شوند، باید مطمئن شویم که ویژگی را قبل از آموزش استاندارد کنیم.

کاهش ویژگی ها با رگرسیون Lasso

چگونگی ساده کردن مدل رگرسیون خطی با کاهش تعداد ویژگی ها:

از رگرسیون lasso استفاده می کنیم.

# Load library
from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
# Load data
boston = load_boston()
features = boston.data
target = boston.target

# Standardize features
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)

# Create lasso regression with alpha value
regression = Lasso(alpha=0.5)

# Fit the linear regression
model = regression.fit(features_standardized, target)

یک ویژگی جالب خطای رگرسیون lasso این است که می تواند ضرایب یک مدل را به صفر برساند و به طور موثر تعداد ویژگی های مدل را کاهش می دهد. به عنوان مثال، در مسئله ما، آلفا را روی 0.5 قرار می دهیم و می بینیم که بسیاری از ضرایب 0 هستند، به این معنی که از ویژگی های مربوطه در مدل استفاده نمی شود:

# View coefficients
model.coef_

array([-0.10697735, 0. , -0. , 0.39739898, -0. ,
2.97332316, -0. , -0.16937793, -0. , -0. ,
-1.59957374, 0.54571511, -3.66888402])

با این حال، اگر مقدار α را به یک مقدار بسیار بالاتر افزایش دهیم، می بینیم که به معنای واقعی کلمه از هیچ یک از ویژگی ها استفاده نمی شود:

# Create lasso regression with a high alpha
regression_a10 = Lasso(alpha=10)
model_a10 = regression_a10.fit(features_standardized, target)
model_a10.coef_

array([-0., 0., -0., 0., -0., 0., -0., 0., -0., -0., -0., 0., -0.])

فایده عملی این اثر این بدان معنی است که می توانیم 100 ویژگی را در ماتریس ویژگی های خود بگنجانیم و سپس، از طریق تنظیم پارامتر α  در lasso، مدلی تولید کنیم که فقط از 10 (به عنوان مثال) تا از مهمترین ویژگی ها استفاده می کند. این امکان را می دهد ضمن کاهش تفسیرپذیری مدل خود، واریانس را هم کاهش دهیم (از آنجا که توضیح ویژگی های کمتر آسان تر است).

 

مثال و توضیحات بالا تقریبا از هر نوع رگرسیون به صورت مختصر بود.

همانطور که در بالا ذکر شد، تجزیه و تحلیل رگرسیون به پیش بینی یک متغیر پیوسته کمک می کند. در دنیای واقعی سناریوهای مختلفی وجود دارد که ما به برخی از پیش بینی های آینده مانند شرایط آب و هوایی ، پیش بینی فروش ، روند بازاریابی و غیره نیاز داریم ، در چنین شرایطی ما به برخی از فن آوری ها نیاز داریم که می تواند با دقت بیشتری پیش بینی ها را انجام دهد. بنابراین برای چنین مواردی ما به تحلیل رگرسیون نیاز داریم که یک روش آماری است و در یادگیری ماشین و علم داده استفاده می شود