خوشه بندی یکی از بخش های هوش منصوعی است که شامل گروه بندی نقاط داده می شود. با توجه به مجموعه ای از نقاط داده ، می توان از یک الگوریتم خوشه بندی برای طبقه بندی هر نقطه داده به یک گروه خاص استفاده کرد. در تئوری ، نقاط داده ای که در یک گروه قرار دارند باید دارای خصوصیات و یا ویژگیهای مشابه باشند ، در حالی که نقاط داده در گروههای مختلف باید دارای خصوصیات و یا ویژگیهای بی شباهت باشند. خوشه بندی روشی از یادگیری بدون نظارت است و یک روش معمول برای تجزیه و تحلیل داده های آماری است که در بسیاری از زمینه ها مورد استفاده قرار می گیرد.
در علم داده ، با دیدن اینکه داده های ما در چه گروه هایی هنگام استفاده از الگوریتم خوشه بندی، قرار می گیرند می توانیم اطلاعات ارزشمندی بدست آوریم. امروز ، ما می خواهیم 5 الگوریتم خوشه بندی محبوب را مورد بررسی قرار دهیم که متخصصین علم داده باید بدانند.
الگوریتم K-Means
K-Means شاید شناخته شده ترین الگوریتم خوشه بندی باشد. در بسیاری از کلاسهای علوم داده مقدماتی و کلاسهای یادگیری ماشین تدریس می شود. درک و اجرای کد آسان است.
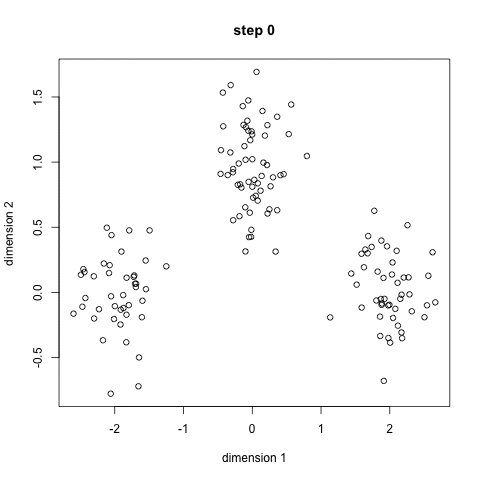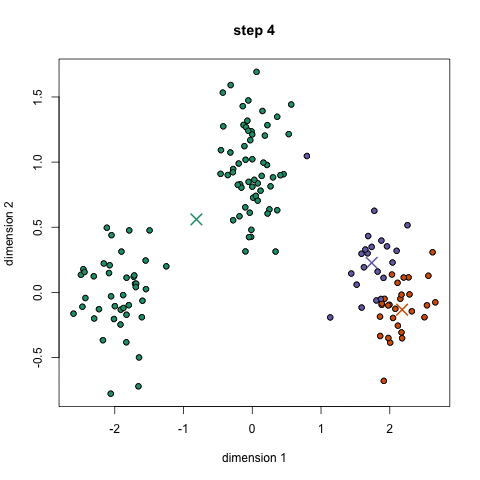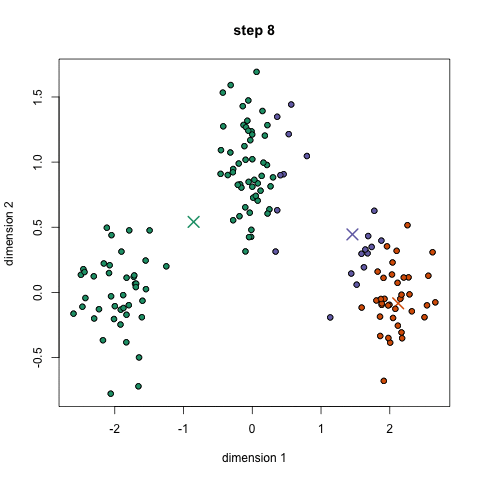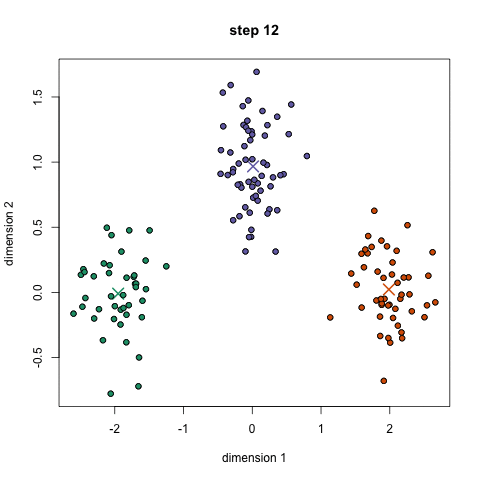
برای شروع ، ابتدا تعداد خوشه (گروه) را برای استفاده انتخاب می کنیم و به طور تصادفی نقاط مربوطه آنها را در فضا قرار می دهیم. سپس هر نقطه داده در گروهی قرار می گیرد که به نقاط تصادفی نزدیک تر است
بر اساس این خوشه بندی ، ما مرکز هر خوشه را به عنوان نقطه جدید انتخاب می کنیم و مرحله قبل را برای خوشه بندی جدید انجام می دهیم.
این مراحل را برای تعداد مشخصی یا تا زمانی که مراکز گروه بین تکرار تغییر چندانی نکنند. تکرار کنید. همچنین می توانید چند مرتبه مراکز گروه را به طور تصادفی مقداردهی کنید .
K-Means این مزیت را دارد که بسیار سریع است ، زیرا تنها محاسبه ما فاصله بین نقاط و مراکز گروه است. بنابراین پیچیدگی خطی O(n) دارد.
از طرف دیگر ، K-Means دو عیب دارد. اول اینکه باید تعداد خوشه ها را انتخاب کنید. ما بعضی اوقات نیاز داریم الگوریتم این کار را برای ما انجام دهد زیرا می خواهیم دیدی از داده ها بدست آوریم. دوم اینکه K-mean با انتخاب تصادفی مراکز خوشه شروع می شود و بنابراین ممکن است نتایج خوشه بندی متفاوتی را در اجرای های مختلف الگوریتم بدست آورد.
K-Medians یکی دیگر از الگوریتم های خوشه بندی مربوط به K-Means است ، با این تفاوت که به جای محاسبه مرکز گروه با استفاده از میانه بردار نقاط جدید را بوجود می آورد. این روش نسبت به نقاط پرت حساسیت کمتری دارد (به دلیل استفاده از Median) اما برای مجموعه داده های بزرگتر بسیار کندتر است زیرا هنگام محاسبه میانه بردار مرتب سازی در هر تکرار مورد نیاز است.
الگوریتم Mean-Shift
الگوریتم Mean-Shift سعی در یافتن مناطق متراکم از نقاط داده دارد.
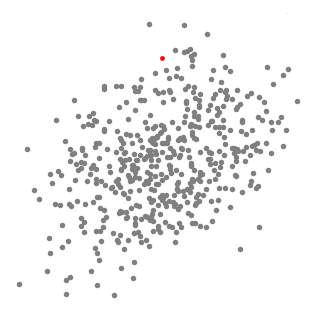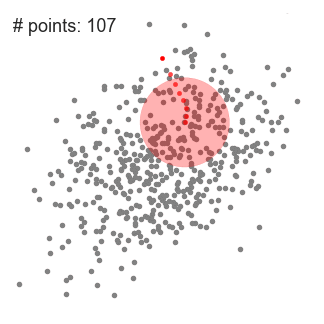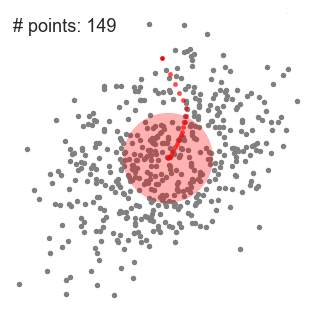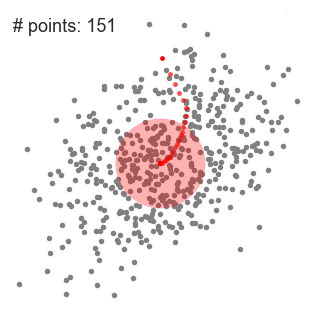
۱- برای توضیح mean-shift، مجموعه ای از نقاط را در فضای دو بعدی مانند تصویر بالا در نظر خواهیم گرفت. ما با یک پنجره کشویی مدور ( circular sliding window) با مرکزیت نقطه C (به طور تصادفی انتخاب شده) و با شعاع r شروع می کنیم. Mean shift یک الگوریتم تپه نوردی (hill-climbing algorithm) یرای انتقال این هسته به به یک منطقه با چگالی بالاتر تا زمان همگرایی است.
۲- در هر تکرار ، پنجره کشویی با انتقال نقطه مرکزی به میانگین نقاط داخل پنجره (دایره) به سمت مناطقی با تراکم بالاتر منتقل می شود. تراکم داخل پنجره کشویی متناسب با تعداد نقاط داخل آن است. به طور طبیعی ، با جابجایی به میانگین نقاط در پنجره ، به تدریج به سمت مناطقی با تراکم نقطه بالاتر حرکت می کند.
۳- ما همچنان پنجره کشویی را مطابق با میانگین ادامه می دهیم تا زمانی که هیچ تغییری نتواند نقاط بیشتری را در داخل هسته جای دهد. گرافیک بالا را مشاهده کنید. ما دایره را حرکت می دهیم تا زمانی که دیگر تراکم را افزایش ندهیم ( تعداد نقاط در پنجره).
۴- این مراحل 1 تا 3 با تعداد زیادی از پنجره های کشویی انجام می شود تا زمانی که همه نقاط در یک پنجره قرار گیرند. هنگامی که چندین پنجره کشویی با هم همپوشانی دارند پنجره حاوی بیشترین نقاط حفظ می شود. داده ها مطابق با پنجره کشویی که در آن سکونت دارند ، خوشه بندی می شوند.
تصویری از کل روند از ابتدا تا انتها با همه پنجره های کشویی در زیر نشان داده شده است. هر نقطه سیاه نشان دهنده مرکز پنجره کشویی است و هر نقطه خاکستری یک نقطه داده است.

برخلاف خوشه بندی K-means نیازی به انتخاب تعداد خوشه ها نیست زیرا mean-shift به صورت خودکار این مسئله را کشف می کند و این یک مزیت برجسته به حساب می آید . مشکل الگوریتم در مبهم بودن انتخاب شعاع پنجره است .
الگوریتم DBSCAN – (Density-Based Spatial Clustering of Applications with Noise)
DBSCAN یک الگوریتم خوشه ای مبتنی بر چگالی است که شبیه به mean-shift است ، اما دارای دو مزیت قابل توجه است. قبل از شروع نگاهی به تصویر زیر بیاندازید.
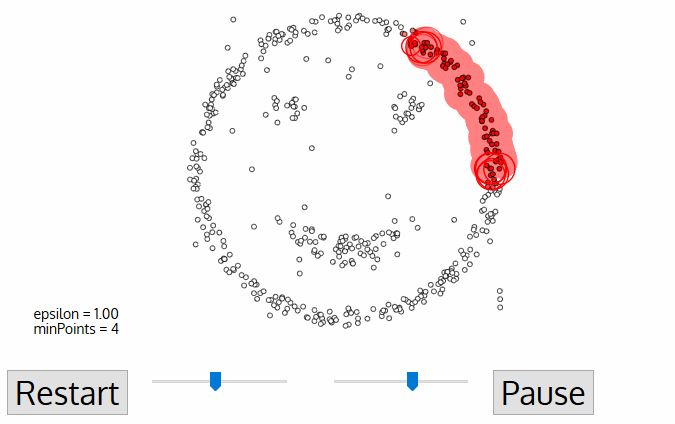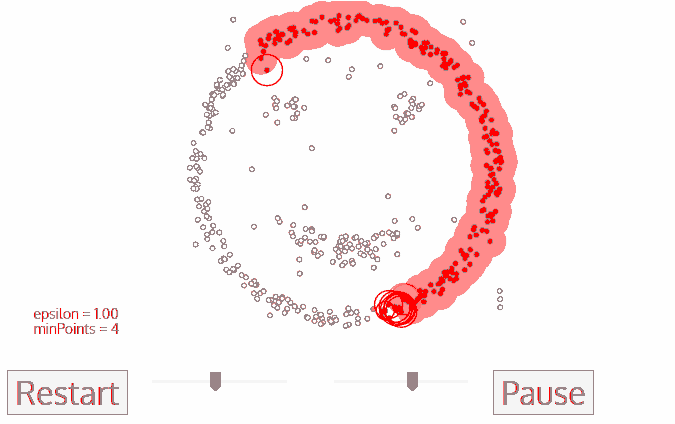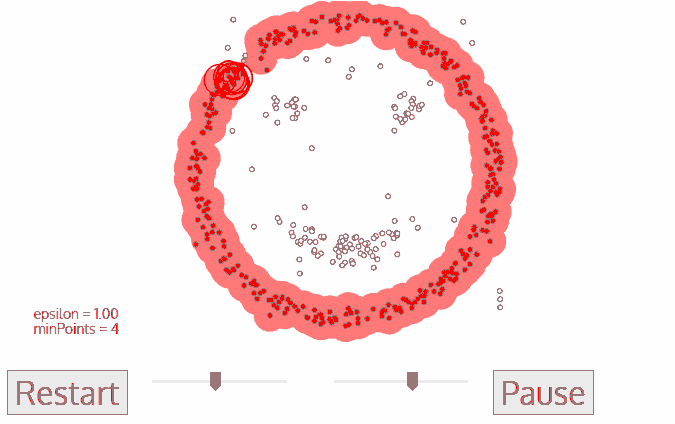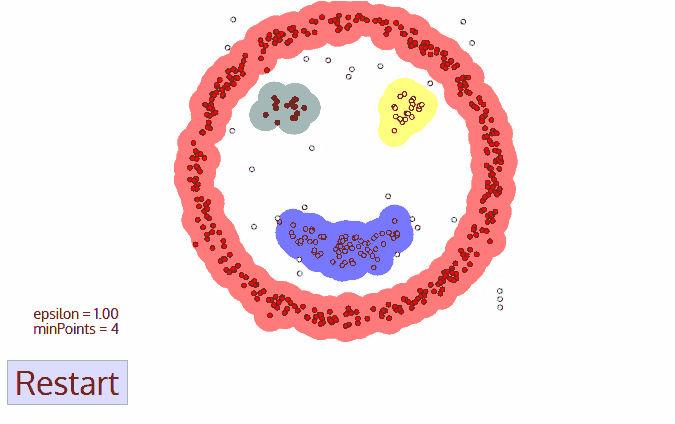
۱- DBSCAN با یک نقطه شروع دلخواه و بازدید نشده شروع می شود . همسایگی این نقطه با استفاده از فاصله اپسیلون ε استخراج می شود (کلیه نقاط که در فاصله ε قرار دارند نقاط همسایگی هستند).
۲- اگر تعداد کافی از نقاط (minPoint) در این محله وجود داشته باشد ، فرآیند خوشه بندی آغاز می شود و نقطه داده فعلی به اولین نقطه در خوشه جدید تبدیل می شود. در غیر این صورت ، این نقطه به عنوان نویز نشان داده می شود (بعداً این نقطه ممکن است به بخشی از خوشه تبدیل شود). در هر دو مورد ، آن نقطه به عنوان “بازدید شده” علامت گذاری شده است.
۳- برای اولین نقطه در خوشه جدید ، نقاط موجود در همسایگی آن نیز بخشی از همان خوشه می شوند و سپس برای تمام نقاط جدیدی که به خوشه اضافه شده اند نیز تکرار می شود.
۴- این روند مراحل 2 و 3 تا زمانی که تمام نقاط موجود در خوشه مشخص شود ، تکرار می شود.
۵- هنگامی که ما با خوشه فعلی کار خود را انجام دادیم ، از یک نقطه بازدید نشده جدید شروع به کشف یک خوشه یا نویز می کنیم . این روند تا زمانی که همه نقاط به عنوان بازدید شده مشخص شوند تکرار می شود. از آنجا که در پایان همه نقاط بازدید شده هستند ، هر نقطه متعلق به یک خوشه یا نویزمشخص می شود.
DBSCAN نسبت به دیگر الگوریتم های خوشه بندی مزایایی دارد. اولاً ، به تعیین تعداد خوشه نیاز ندارد. همچنین بر خلاف mean-shift که حتی اگر نقطه داده بسیار متفاوت باشد آنرا به درون یک خوشه می اندازد ، نقاط دور را به عنوان نویز شناسایی می کند. علاوه بر این ، می تواند خوشه های با اشکال پیچیده را به خوبی پیدا کند.
اشکال اصلی DBSCAN این است که وقتی خوشه ها از چگالی مختلفی برخوردار هستند عملکرد آن به خوبی قبل نیست. این بدان دلیل است که تنظیم آستانه فاصله ε و minPoint برای شناسایی نقاط محله در هنگام تغییر چگالی از خوشه به خوشه دیگر متفاوت خواهد بود. این اشکال در داده های با بعد بسیار زیاد (very high-dimensional data) نیز اتفاق می افتد زیرا دوباره آستانه فاصله ε برای برآورد چالش برانگیز می شود.
خوشه بندی Expectation–Maximization) EM) با استفاده ازمدل Gaussian) GMM (Mixture Models
یکی از اشکالات عمده الگوریتم K-Means استفاده ساده از مقدار متوسط برای مرکز خوشه است. با دیدن تصویر زیر می فهمیم که چرا این بهترین روش برای انجام کارها نیست. در سمت چپ ، برای چشم انسان کاملاً واضح به نظر می رسد که دو خوشه دایره ای با شعاع متفاوت با مرکزیت یکسان وجود دارد. K-Means نمی تواند از عهده این کار برآید زیرا مقادیر میانگین خوشه ها بسیار نزدیک به هم هستند. K-Means همچنین در مواردی که خوشه ها دایره ای نیستند دچار مشکل می شود.

مدل های GMM انعطاف پذیری بیشتری نسبت به K-Means به ما می دهند. با GMM ها فرض می کنیم که نقاط داده توزیع گاوسی (توزیع نرمال)هستند. با این فرض ما کمتر از قبل محدود می شویم. به این ترتیب ، ما دو پارامتر برای توصیف شکل خوشه ها داریم: میانگین و انحراف معیار. با مثالی در دو بعد ، این بدان معناست که خوشه ها می توانند هر نوع شکل بیضوی داشته باشند (از آنجا که در هر دو جهت x و y انحراف معیار داریم). بنابراین، هر توزیع گاوسی به یک خوشه منفرد اختصاص یافته است.
برای یافتن پارامترهای Gaussian برای هر خوشه (به عنوان مثال میانگین و انحراف معیار) ، ما از یک الگوریتم بهینه سازی به نام Expectation – Maximization (EM) استفاده خواهیم کرد. به عنوان تصویری از اتصال گوسی ها به خوشه ها ، به شکل زیر نگاه کنید. سپس می توانیم روند خوشه بندی Expectation – Maximization را با استفاده از GMM ها ادامه دهیم.
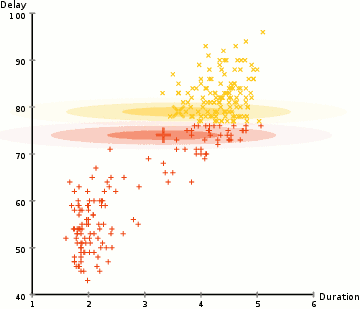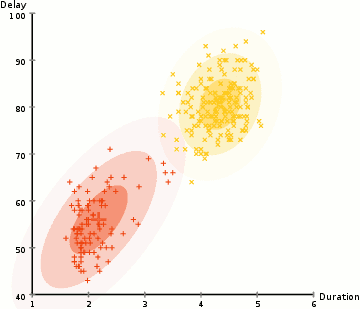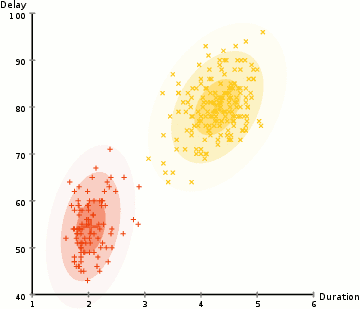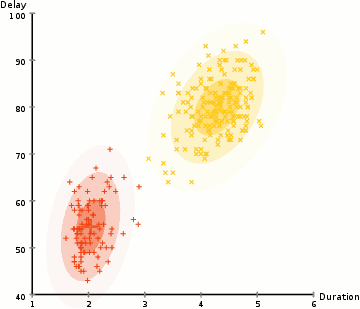
۱- ما با انتخاب تعداد خوشه (مانند K-Means) و مقداردهی تصادفی پارامترهای توزیع گاوسی برای هر خوشه شروع می کنیم. با نگاهی گذرا به داده ها می توان پارامترهای اولیه را مقداردهی کرد ، اگرچه همانطور که در نمودار بالا مشاهده می شود ، این کار 100٪ ضروری نیست زیرا Gaussians کار ما را بسیار ضعیف آغاز می کند اما به سرعت بهینه می شود.
۲-با توجه به این که هر خوشه دارای توزیع گاوسی است ، احتمال متعلق بودن هر داده به یک خوشه خاص را محاسبه کنید. هرچه یک نقطه به مرکز Gaussian نزدیکتر باشد ، احتمال تعلق آن به آن خوشه بیشتر است. زیرا با توزیع گوسی فرض می کنیم که بیشتر داده ها به مرکز خوشه نزدیکتر هستند.
۳- بر اساس این احتمالات ، ما پارامترهای توزیع گاوسی را محاسبه می کنیم به گونه ای که احتمالات نقاط داده را در خوشه ها به حداکثر برسانیم. ما این پارامترهای جدید را با استفاده از مجموع وزنی از موقعیت های نقطه داده محاسبه می کنیم که وزن، احتمال نقطه داده مربوط به آن خوشه خاص است. برای توضیح از نظر بصری ، می توانیم به گرافیک بالا ، به ویژه خوشه زرد ، نگاهی بیندازیم. توزیع به صورت تصادفی در اولین تکرار آغاز می شود ، اما می توان دریافت که بیشتر نقاط زرد در سمت راست آن توزیع قرار دارند. وقتی ما مجموع وزنی را با توجه به احتمالات محاسبه می کنیم ، حتی اگر در نزدیکی مرکز چند نقطه وجود داشته باشد ، بیشتر آنها در سمت راست قرار دارند. بنابراین به طور طبیعی میانگین توزیع به آن طرف نزدیکتر می شود. همچنین می توانیم ببینیم که بیشتر نقاط “بالا راست به پایین چپ” هستند. بنابراین انحراف معیار تغییر می کند و بیضی ایجاد می کند ، تا مجموع وزنی را به حداکثر برساند.
۴- مراحل 2 و 3 تا زمان همگرایی تکرار می شود ، تا جایی که توزیع ها از به هنگام تکرار تغییر چندانی نکنند.
استفاده از GMM ها ۲ مزیت اصلی دارد. اولاً GMM ها از نظر کوواریانس خوشه ای بسیار انعطاف پذیر تر از K-Means هستند. با توجه به پارامتر انحراف استاندارد ، خوشه ها می توانند به غیر از محدود شدن به دایره ها، هر شکل بیضی به خود بگیرند. K-Means در حقیقت یک مورد خاص از GMM است که در آن کوواریانس هر خوشه در تمام ابعاد به 0 می رسد. ثانیا، از آنجا که GMM ها از احتمالات استفاده می کنند ، می توانند خوشه های مختلفی را برای هر نقطه داده داشته باشند. بنابراین اگر یک نقطه داده در وسط دو خوشه با هم تداخل داشته باشد ، می توانیم خوشه آن را به راحتی تعریف کنیم و بگوییم که آن X درصد به کلاس 1 و Y درصد به کلاس 2 است. بنابراین GMM ها از عضویت مختلط پشتیبانی می کنند.
الگوریتم خوشهبندی فازی ( Fuzzy clustering)
یک الگوریتم خوشهبندی جهت تقسیم داده ها به خوشه هایی بیش از یک خوشه می باشد.در این خوشهبندی هر داده به درجه خاصی از هر خوشه متعلق است و با توجه به درجه تعلق حضور یک داده به یک خوشه مشخص می گردد.خوشه بندی فازی سی-مینز (FCM) توسط جی سی دانز در سال ۱۹۷۳ آماده شدو در سال ۱۹۸۱ ارتقا داده شد
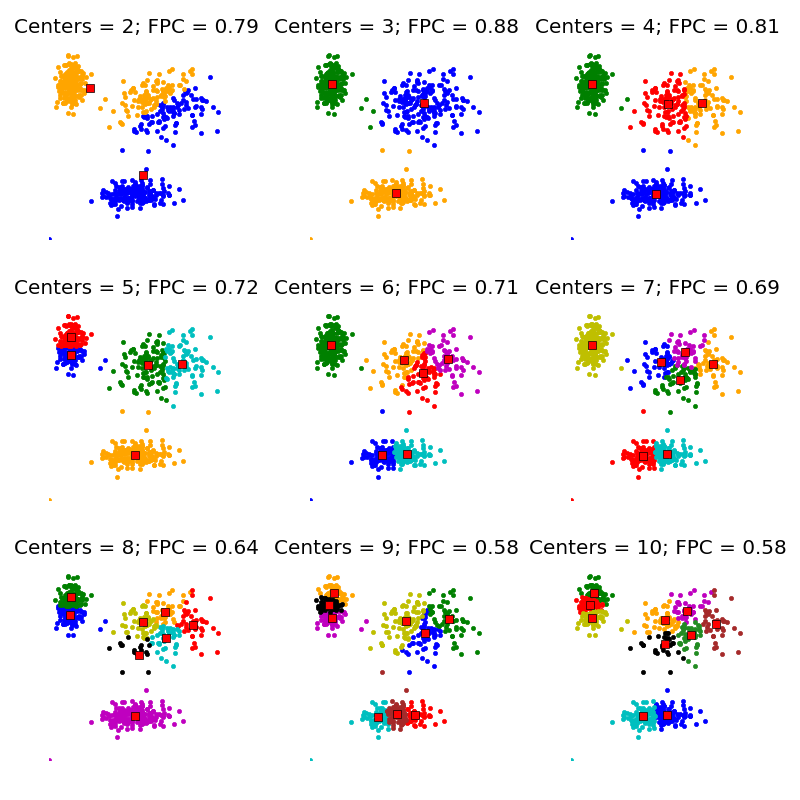
در الگوریتم خوشه بندی فازی FCM باید تعداد و مراکز خوشه ها توسط کاربر در ابتدا مشخص شوند. کیفیت این الگوریتم بشدت به تعداد اولیه خوشه ها و مکان اولیه مراکز خوشه ها بستگی دارد. هدف از خوشه بندی فازی استخراج مدل های فازی از داده هاست. کاربردهای متعدد خوشه بندی فازی در تحلیل دادهها و تشخیص الگو و نیز زمینه های پژوهشی موجود در این زمینه از جمله استفاده از آن در حل مسائل مسیریابی، تخصیص و زمان بندی نیاز به مطالعه الگوریتم های موجود و بهبود و اصلاح آن ها را آشکارتر می نماید. در مجموعه های کلاسیک یک عضو از مجموعه مرجع یا عضوی از مجموعه A است یا عضو مجموعه A نیست. مثلا در مجموعه مرجع اعداد حقیقی عدد 2. 5 عضو مجموعه اعداد صحیح نمی باشد حال آنکه عدد 2 عضو این مجموعه است. اما در مجموعه انسان های جوان و پیر سوالی که مطرح می شود این است که آیا فردی با سن 25 جزء مجموعه جوان است یا پیر . نمی توان بطور قطع و یقین مرزی برای انسان های جوان و پیر در نظر گرفت. دلیل آن هم این است که اگر فرضا 35 جوان محسوب شود 36 نیز می تواند جوان باشد و همینطور 37 و 38 و غیره. در واقع در اینجا با مفهوم عدم قطعیت مواجه هستیم. ما خودمان نیز از عدم قطعیت در زندگی روزمره بارها استفاده کرده ایم مثلا هوای سرد، آب داغ و غیره. در واقع تمامی مثالهای بالا مثالهایی از مجموعه های فازی می باشند
مراحل الگوریتم خوشه بندی فازی به خوشهبندی کی-میانگین شباهت دارد و به شرح زیر است:
- تعیین تعداد خوشهها در یک مجموعه داده
- تخصیص تصادفی هر داده به خوشه مربوط به آن
- تکرار مکرر خوشه جهت پوشش همه دادهها در خوشههای نزدیکتر
- محاسبه مرکز خوشههای هر خوشه
- تشخیص حضور هر داده در هر خوشه
الگوریتم Hierarchical
الگوریتم های خوشه بندی سلسله مراتبی (Hierarchical) در 2 دسته: از بالا به پایین یا پایین به بالا قرار می گیرند. الگوریتم های پایین به بالا هر نقطه داده را در ابتدا به عنوان یک خوشه واحد در نظر می گیرند و سپس به طور پی در پی جفت خوشه ها را ادغام می کنند (یا جمع می شوند) تا زمانی که همه خوشه ها در یک خوشه واحد ادغام می شوند که شامل تمام نقاط داده است. از این رو خوشه بندی سلسله مراتبی از پایین به بالا خوشه جمع بندی سلسله مراتبی یا HAC گفته می شود. این خوشه های سلسله مراتبی به عنوان یک درخت (یا dendrogram) نشان داده می شود. ریشه درخت یک خوشه منحصر به فرد است که همه نمونه ها را جمع می کند ، برگهای خوشه فقط یک نمونه هستند. قبل از رفتن به مراحل الگوریتم ، تصویر زیر را بررسی کنید.
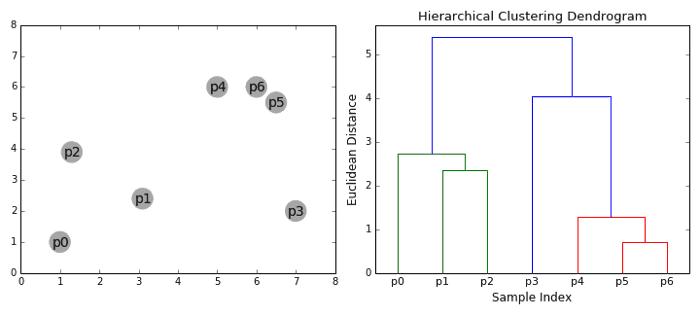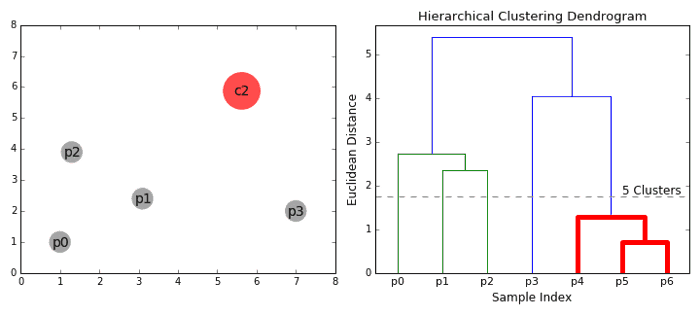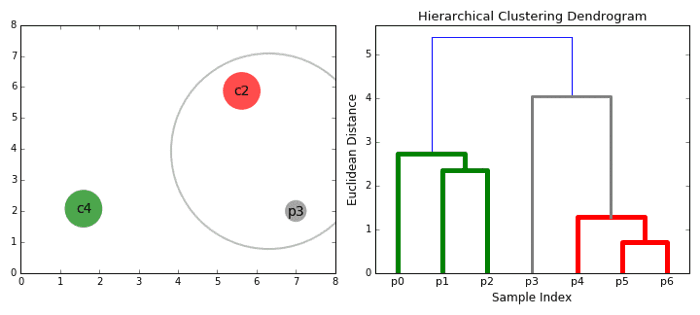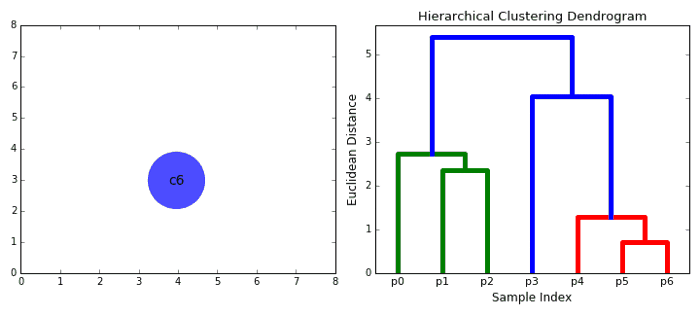
۱- ما با پردازش هر نقطه داده به عنوان یک خوشه واحد شروع می کنیم ، یعنی اگر X داده در مجموعه داده ما وجود داشته باشد ، ما X خوشه داریم. سپس یک معیار فاصله را انتخاب می کنیم که فاصله بین دو خوشه را اندازه می گیرد. به عنوان مثال ، ما فاصله بین دو خوشه را میانگین فاصله بین نقاط داده در خوشه اول و نقاط داده در خوشه دوم تعریف می کنیم.
۲- در هر تکرار ، دو خوشه را با هم ترکیب می کنیم. دو خوشه ای که باید ترکیب شوند خوشه هایی با کمترین فاصله هستند. و بنابراین بیشترین شباهت را دارند و باید با هم ترکیب شوند.
۳- مرحله ۲ را تکرار می کنیم تا زمانی که به ریشه درخت برسیم ، یعنی فقط یک خوشه داریم که شامل تمام نقاط داده است. به این ترتیب می توانیم انتخاب کنیم که در پایان چه تعداد خوشه می خواهیم ، به سادگی با انتخاب زمان متوقف کردن ترکیب خوشه ها
خوشه بندی سلسله مراتبی نیازی به تعیین تعداد خوشه ندارد و حتی می توانیم بعد از ساختن درخت تعیین کنیم تعداد خوشه ها چقدر باشد مناسب تر است. علاوه بر این ، الگوریتم به انتخاب اندازه فاصله حساس نیست. در حالی که در الگوریتم های دیگر خوشه بندی ، انتخاب اندازه فاصله بسیار مهم است. یک مورد استفاده از روشهای خوشه بندی سلسله مراتبی این است که داده ها دارای ساختار سلسله مراتبی هستند و شما می خواهید سلسله مراتب را بازیابی کنید.دیگر الگوریتم های خوشه بندی نمی توانند این کار را انجام دهند. این مزایای خوشه بندی سلسله مراتبی بهای کمتری دارد ، زیرا برخلاف پیچیدگی خطی K-Means و GMM دارای پیچیدگی زمانی O (n³) است.