درک الگوریتم جنگل تصادفی (Random Forest)

بخش بزرگی از یادگیری ماشینی طبقه بندی است – ما می خواهیم بدانیم که مشاهده مربوط به چه کلاسی است. توانایی طبقه بندی دقیق مشاهدات برایکسب و کارهای مختلف مانند پیش بینی اینکه آیا کاربر خاصی محصولی را خریداری می کند یا پیش بینی اینکه وام داده شده پس داده خواهد شدیا خیر ، بسیار ارزشمند است.
علم داده مجموعه ای از الگوریتم های طبقه بندی مانند رگرسیون لجستیک ، ماشین بردار پشتیبان (SVM) ، درخت تصمیم را فراهم می کند. یکی از بهترین ها ،الگوریتم طبقه بندی جنگل تصادفی است
در این پست ، ما نحوه کار درختان تصمیم ، چگونگی ترکیب درخت های تصمیم برای ایجاد یک جنگل تصادفی را بررسی خواهیم کرد و در نهایت می فهمیم که چرا جنگل های تصادفی در کارهایی که انجام می دهد بسیار خوب عمل می کند.

درخت تصمیم – Decision Tree

در اینجا یک نگاه اجمالی به الگوریتم درخت تصمیم می کنیم، زیرا عنصر اصلی تشکیل دهنده جنگل تصادفی می باشد.

احتمالاً درک نحوه کار درخت تصمیم از طریق یک مثال بسیار آسان تر است.
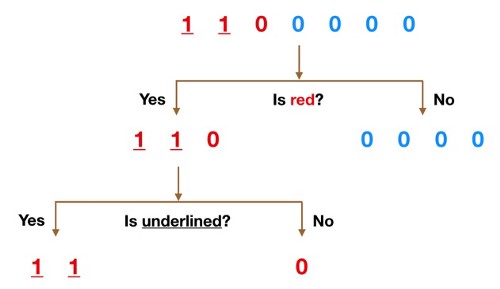
تصور کنید که مجموعه داده ما از اعداد بالای شکل تشکیل شده است. ما ۲ تا ۱ و ۵ تا ۰ داریم (۱ و ۰ کلاس ما هستند) و تمایل داریم کلاس ها را با استفاده از ویژگی های آنها جدا کنیم . یک از ویژگی ها رنگ (قرمز در مقابل آبی) و دیگری اینکه آیا زیر مشاهدات خط کشیده شده است یا خیر. بنابراین چگونه می توانیم این کار را انجام دهیم؟

در ابتدا داده های خود را براساس ویژگی رنگ تقسیم می کنیم، و کار خود را با این سوال شروع میکنیم که آیا داده ما قرمز است؟

شاخه No (آبی ها) همه اعداد ۰ هستند بنابراین ما کار را در آنجا خاتمه می دهیم ، اما شاخه Yes ما هنوز می تواند بیشتر تقسیم شود. اکنون می توانیم از ویژگی دوم استفاده کنیم و بپرسیم ، “آیا این مورد خط زیرین دارد؟” .

دو عدد 1 که خط زیرین دارند از زیرشاخه Yes پایین می آیند و 0 که زیرخط ندارد از زیر شاخه سمت راست پایین می رود و در اینجا کار ما تمام است. درخت تصمیم ما توانست از دو ویژگی برای تقسیم کامل داده ها استفاده کند.

بدیهی است که در زندگی واقعی داده های ما اینقدر تمیز نخواهند بود اما منطقی که درخت تصمیم به کار می برد همان است. در هر گره ، از شما می پرسد -چه ویژگی به من امکان می دهد مشاهدات موجود را به گونه ای تقسیم کنم که گروههای حاصله تا حد ممکن از یکدیگر متفاوت باشند (و اعضای هر گروه فرعی حاصل از آن تا حد امکان شبیه به یکدیگر باشند)؟

الگوریتم جنگل تصادفی

جنگل تصادفی، همانطور که از نام آن پیداست ، از تعداد زیادی درخت تصمیم تشکیل شده است که به عنوان یک مجموعه فعالیت می کنند. هر درخت جداگانه در جنگل تصادفی یک پیش بینی را انجام می دهد و کلاس با بیشترین آرا پیش بینی مدل ما می شود (شکل زیر را ببینید).

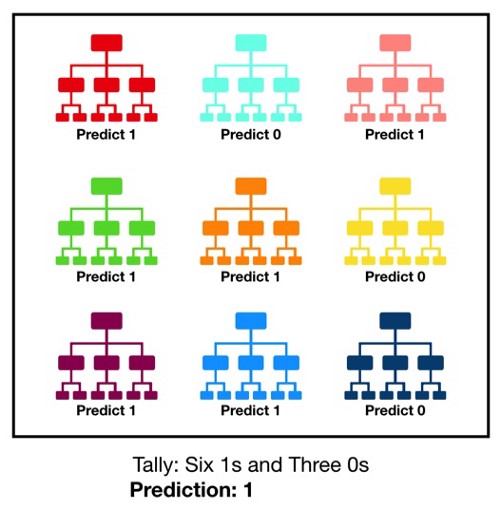
مفهوم جنگل تصادفی یک مفهوم ساده اما قدرتمند است – خرد جمعی. در علم داده دلیل اینکه مدل جنگل تصادفی بسیار خوب عمل می کند این است که:
تعداد زیادی از مدلهای نسبتاً غیر همبسته (درختان) که به عنوان کمیته فعالیت می کنند ،عملکرد بهتری از هر یک از مدلهای منفرد دارد .
نکته اصلی در همبستگی کم بین مدل ها است. مدل های غیر همبسته می توانند پیش بینی های گروهی را تولید کنند کهاز هر پیش بینی فردی دقیق تر است. دلیل این اثر شگفت انگیز این است که درختان از یکدیگر در برابر خطاهای فردی خود محافظت می کنند (به شرطی که همه آنها در یک جهت اشتباه نکنند). گرچه ممکن است برخی از درختان اشتباه کنند ، اما بسیاری از درختان دیگر درست پیش بینی خواهند کرد ، بنابراین به عنوان یک گروه ، درختان قادر به حرکت در مسیر صحیح هستند. بنابراین پیش نیازهای جنگل تصادفی برای عملکرد خوب عبارتند از:

ویژگیهای ما باید دارای سیگنالهایی باشند تا مدلهای ساخته شده با استفاده از این ویژگیها بهتر از حدس تصادفی عمل کنند.
پیش بینی ها (و بنابراین اشتباهات) توسط درختان جداگانه باید ارتباط کمی با یکدیگر داشته باشند.

مثالی از اینکه چرا نتایج غیر همبسته بسیار عالی هستند

تصور کنید که ما بازی زیر را انجام می دهیم:
من از یک مولد توزیع یکنواخت اعداد تصادفی برای تولید یک عدد استفاده می کنم.
اگر عددی که من تولید می کنم بیشتر یا برابر با 40 باشد ، شما برنده می شوید (بنابراین شما 60٪ شانس پیروزی دارید) و من مقداری پول به شما پرداخت می کنم. اگر زیر 40 باشد ، من برنده می شوم و شما همین مبلغ را به من پرداخت می کنید.
اکنون من گزینه های زیر را به شما پیشنهاد می دهم. ما یا می توانیم:

1. بازی 1 – 100 بار بازی کنید ، هر بار 1 دلار شرط بندی کنید.
2. بازی 2 – 10 بار بازی کنید ، هر بار 10 دلار شرط بندی کنید.
3. بازی 3— یک بار بازی کنید ، 100 دلار شرط بندی کنید.

کدام را انتخاب می کنید؟ امید ریاضی هر ۳ بازی یکسان است.

Expected Value Game 1 = (0.60*1 + 0.40*-1)*100 = 20

Expected Value Game 2= (0.60*10 + 0.40*-10)*10 = 20

Expected Value Game 3= 0.60*100 + 0.40*-100 = 20

توزیع ها چطور؟ بیایید نتایج را با یک شبیه سازی مونت کارلو تجسم کنیم (ما 10،000 شبیه سازی از هر نوع بازی را اجرا خواهیم کرد ؛ به عنوان مثال ، ما 10،000 بار بازی را شبیه سازی خواهیم کرد).

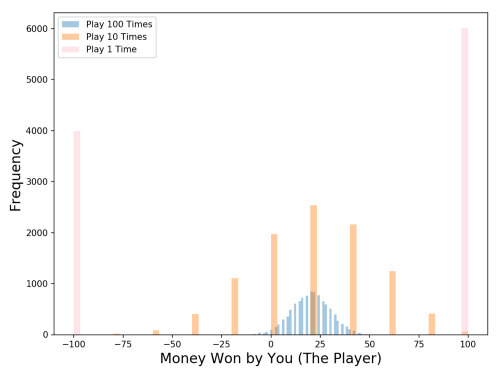
نگاهی به نمودار بیاندازید – حالا کدام بازی را انتخاب می کنید؟ حتی اگر امید ریاضی مورد انتظار یکسان باشند ، توزیع نتیجه بسیار متفاوت است.

بازی 1 (جایی که 100 بار در آن بازی می کنیم) بهترین شانس را برای کسب درآمد دارد – از 10 هزار شبیه سازی که من انجام دادم ، شما در 97 درصد آنها درآمد کسب می کنید! برای بازی 2 (جایی که ما 10 بار در آن بازی می کنیم) با 63 درصد شبیه سازی ، کاهش چشمگیر (و افزایش شدید احتمال از دست دادن پول) درآمد کسب می کنید. و بازی 3 که ما فقط یک بار بازی می کنیم ، همانطور که انتظار می رفت در 60٪ از شبیه سازی ها درآمد کسب می کنید.

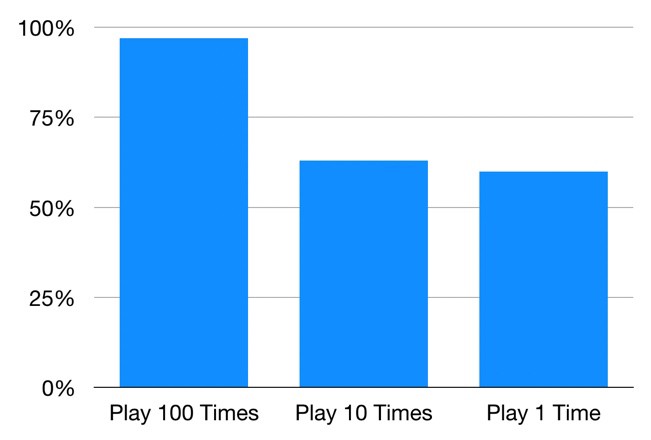
بنابراین حتی اگر بازی ها ازامید ریاضی یکسان برخوردار باشند ، توزیع نتیجه آنها کاملاً متفاوت است. هر چقدر شرط 100 دلاری خود را به تعدا بازی های بیشتر تقسیم کنیم ، می توان اطمینان بیشتری از کسب درآمد داشت. به این دلیل که هر بازی مستقل از بازی های دیگر است.
جنگل تصادفی مانند همین مثال است- هر درخت مانند یک بازی است. ما دیدیم که چطور شانس ما برای کسب درآمد هرچه بیشتر بازی کنیم بیشتر می شود. به همین ترتیب ، با یک مدل جنگل تصادفی ، شانس ما برای پیش بینی صحیح با تعداد درختان غیر همبسته در مدل ما افزایش می یابد.

اطمینان از تنوع بخشیدن به مدلها

بنابراین چگونه جنگل تصادفی تضمین می کند که رفتار هر یک از درختان با رفتار درختان دیگر در مدل خیلی همبسته نباشد؟ از دو روش زیر استفاده می کند:

بگینگ (Bagging): درخت های تصمیم نسبت به داده هایی که روی آنها آموزش داده می شود بسیار حساس هستند – تغییرات کوچک در مجموعه آموزش می تواند باعث ایجاد ساختارهای مختلف درختی شود. جنگل تصادفی از این مزیت استفاده می کند و اجازه می دهد تا هر درخت از مجموعه داده هابه طور تصادفی با جایگذاری نمونه برداری کند و در نتیجه درختان مختلف ایجاد شود. این فرآیند به کیسه بندی معروف است.
توجه داشته باشید که با استفاده از بگینگ ، ما داده های آموزش را به قطعات کوچکتر تقسیم نمی کنیم و هر درخت را روی یک تکه متفاوت آموزش نمی دهیم. در عوض ، اگر نمونه ای از اندازه N داشته باشیم ، هنوز در حال تغذیه هر درخت با مجموعه ای از اندازه N هستیم . اما به جای داده های اصلی آموزش ، ما یک نمونه تصادفی از اندازه N را با جایگذاری می گیریم. به عنوان مثال ، اگر داده های آموزش ما [1 ، 2 ، 3 ، 4 ، 5 ، 6] باشد ، ممکن است به یکی از درختان خود لیست زیر را ارائه دهیم [1 ، 2 ، 2 ، 3 ، 6 ، 6]. توجه داشته باشید که هر دو لیست دارای طول شش هستند و “2” و “6” هر دو در داده های آموزش برای درخت خود تکرار می شوند (زیرا ما با جایگذاری نمونه می گیریم).

تصادفی بودن ویژگی : در یک درخت تصمیم عادی ، هنگام تقسیم یک گره ، ما هر ویژگی ممکن را در نظر می گیریم و یکی از مواردی را که بیشترین تفکیک را بین مشاهدات گره سمت چپ در مقابل گره راست ایجاد می کند ، انتخاب می کنیم. در مقابل ، هر درخت در یک جنگل تصادفی فقط می تواند از مجموعه تصادفی ویژگی ها انتخاب کند. این کار تنوع بیشتری در میان درختان موجود در مدل ایجاد می کند و در نهایت منجر به همبستگی کمتری در میان درختان و تنوع بیشتر می شود.

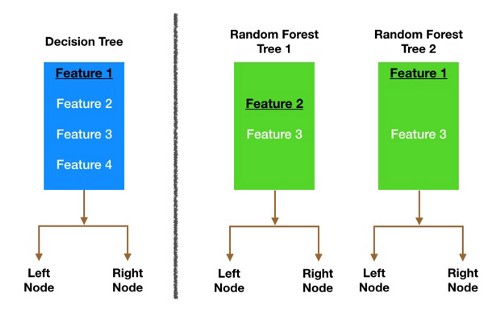
بیایید یک مثال را مرور کنیم – در تصویر بالا ، درخت تصمیم سنتی (به رنگ آبی) می تواند هنگام تصمیم گیری در مورد تقسیم گره ، از هر چهار ویژگی انتخاب کند. تصمیم به انتخاب ویژگی 1 (سیاه و زیر خط دار) می گیرد زیرا داده ها را به گروههایی تقسیم می کند که تا حد امکان از هم جدا شده اند.

حالا بیایید نگاهی به جنگل تصادفی ما بیندازیم. ما فقط دو درخت جنگل را در این مثال بررسی خواهیم کرد. هنگامی که درخت جنگل تصادفی 1 را بررسی می کنیم ، متوجه می شویم که فقط می تواند ویژگی های 2 و 3 را (به طور تصادفی انتخاب شده) برای تصمیم تقسیم گره در نظر بگیرد. ما از درخت تصمیم سنتی خود (به رنگ آبی) می دانیم که ویژگی 1 بهترین ویژگی برای تقسیم است ، اما درخت 1 نمی تواند ویژگی 1 را ببیند بنابراین مجبور می شود ویژگی 2 (سیاه و زیر خط) را انتخاب کند. از طرف دیگر ، درخت 2 فقط ویژگی های 1 و 3 را می بیند ، بنابراین می تواند ویژگی ۱ را انتخاب کند

بنابراین در جنگل تصادفی خود ، درختانی استفاده می شوند که نه تنها در مجموعه های مختلف داده آموزش دیده اند (به لطف بگینگ) بلکه از ویژگی های مختلفی برای تصمیم گیری استفاده می کنند.

و اینگونه، درختان نامرتبط ایجاد می شود تا یکدیگر را از خطاها محافظت کنند.